Chapter 1: The Challenge of the Cambridge Mathematics Tripos

The Cambridge Mathematics Tripos is renowned for being one of the most demanding math programs globally. Unlike many other academic paths, which often utilize modular assessments on specialized subjects, the Cambridge Tripos conducts its examinations annually. This involves four three-hour papers that cover a vast range of topics. First-year students engage in Part IA, second-year students tackle Part IB, and final-year students take Part II. There is also an optional third year, known as Part III, for those who excel in the earlier parts.

Recently, while reviewing Paper 1 from Part II, I encountered a statistics question that involved R programming. I was intrigued and decided to share it here. I've broken it down into sections for you to try answering it before I present my solutions.

Section 1.1: Part (a) Analysis

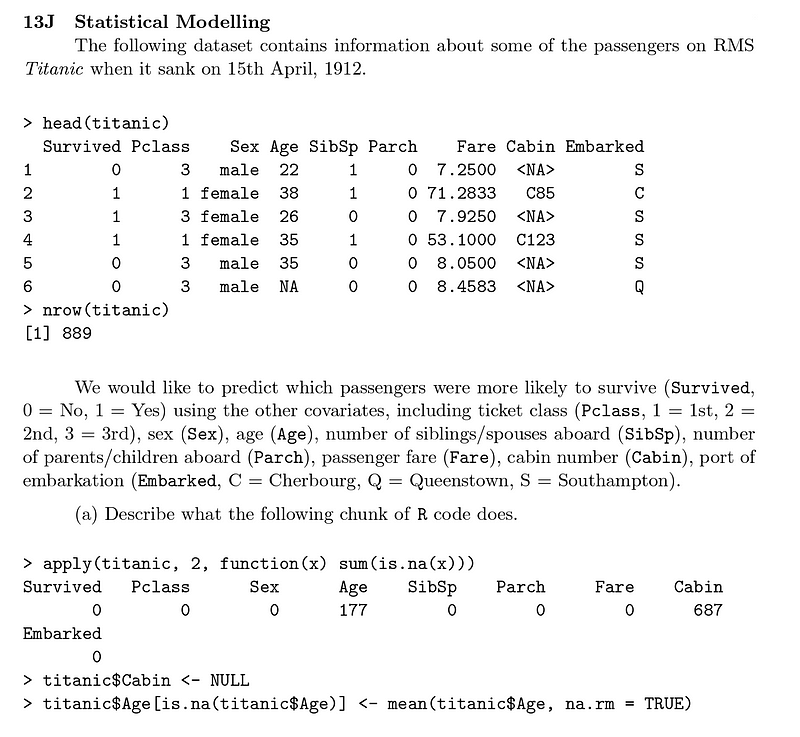
In my response to this part, I noted that:

• The first line determines the count of missing values across each column of the Titanic dataset.
• The second line excludes the Cabin column from the dataset.
• The third line fills the missing values in the Age column by calculating the mean of the existing (non-missing) values.

Section 1.2: Part (b) Insights

For this part, my solution highlighted that the generalized linear model in question is a binomial logistic regression model expressed as follows:

P(Survived = 1|X) = ?(?X)

where ?(u) = e^u/(1 + e^u), representing the logistic function, X denotes the covariate vector, and ? signifies the parameter vector.

The parameters are determined by maximizing the log-likelihood function:

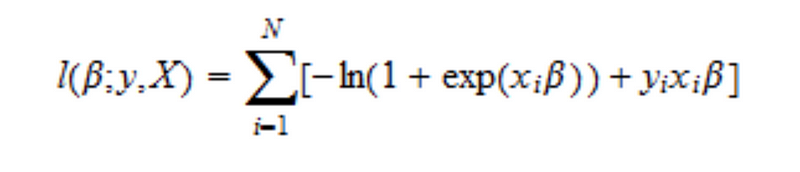
The AIC formula is given by:

AIC = 2k - 2ln(L’)

where L’ is the peak value of the likelihood function and k is the number of covariates.

The backwards stepwise algorithm begins with all covariates in the model. At each step, the least significant variable (the one with the highest p-value) is removed, and the AIC for the new model is computed. This process continues until the minimum AIC is identified. Since the AIC penalizes unnecessary covariates, achieving a minimal AIC leads to a more efficient final model.

Chapter 2: Further Analysis of Parts (c) and (d)

My conclusion for these parts is as follows: Although the median deviance residual is slightly left of zero, the first quartile aligns closely with what is expected in a normal distribution (-0.59 vs -0.67), and the third quartile also approximates a normal distribution (0.62 vs 0.67). Thus, while there is a minor left skew, a dispersion parameter of 1 remains a reasonable estimate.

Typically, the dispersion parameter for a GLM is computed by dividing the scaled deviance of the fitted model by the degrees of freedom of the model (which is the sample size minus the number of predictors). For this logistic regression model, the log-likelihood of a saturated model is zero, simplifying to the residual deviance divided by the degrees of freedom, which equals 784.21/880 = 0.89.

Feel free to share your thoughts on this exam question and whether you agree with my interpretations in the comments below.

This video offers crucial strategies to excel in your Paper 3 exam, ensuring you grasp essential concepts and techniques.

In this clearer recording, the video provides vital tips to help you navigate Paper 3 successfully, enriching your understanding and exam readiness.