Gamma Exposure and Random Forest: A New Era in S&P 500 Predictions
Written on
Chapter 1: Understanding Gamma Exposure
Gamma exposure is an essential concept in options trading, particularly in quantitative finance. It measures how sensitive an option’s price is to fluctuations in the price of the underlying asset. Specifically, gamma assesses the rate of change in an option’s delta, which indicates how the option's value reacts to shifts in the underlying asset’s price.
This article will delve into historical gamma exposure data and construct a random forest model aimed at forecasting the S&P 500 returns based on these gamma exposure values.
The Gamma Exposure Index
The gamma exposure index (GEX) highlights how option contracts react to variations in the underlying price. When market imbalances arise, market makers’ hedging activities can lead to significant price movements, such as short squeezes. The absolute value of the GEX indicates the volume of shares that will be bought or sold to counter a 1% move in the opposite direction of the trend. For instance, a 1% price increase with a GEX of 5 million suggests that 5 million shares will enter the market to drive prices downward as a hedge.
The following graph illustrates the historical trends of the GEX.
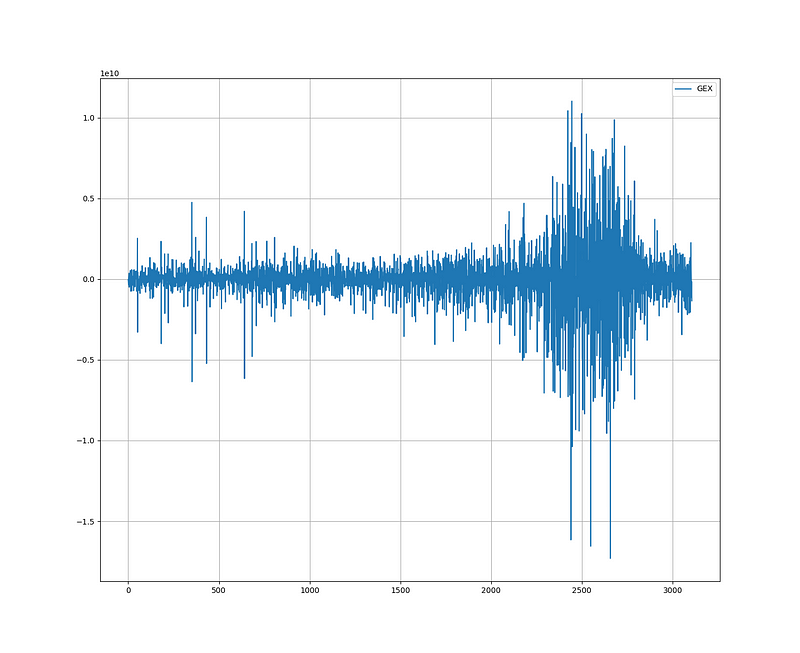
The GEX is regularly published by SqueezeMetrics and is available for free download.
Incorporating Fibonacci Analysis
Fibonacci analysis plays a vital role in technical analysis. Discover how to utilize advanced Fibonacci techniques, recognize market patterns, and apply Fibonacci indicators in my latest book, The Fibonacci Trading Book.

Chapter 2: Developing the Prediction Algorithm
Our objective is to leverage GEX values as inputs for a random forest algorithm to model the returns of the S&P 500 index. Simply put, we are creating a machine learning model that uses the GEX to forecast whether the S&P 500 will trend up or down. Here are the steps involved:
- Install Selenium and download the Chrome WebDriver, ensuring compatibility with your version of Google Chrome.
- Use the provided script to automatically gather historical GEX and S&P 500 data.
- Shift the index values by a specified number of lags (20 in this case) and clean the data.
- Split the dataset into training and testing subsets.
- Fit the random forest regression algorithm and make predictions.
- Evaluate performance using the hit ratio (accuracy).
Note: The index is stationary, meaning it lacks a trending character that would make it unsuitable for regression analysis.
Here’s the code to implement the research:
# Importing Libraries
import pandas as pd
import numpy as np
from selenium import webdriver
from selenium.webdriver.common.by import By
from sklearn.ensemble import RandomForestRegressor
import matplotlib.pyplot as plt
# Initializing Chrome
driver = webdriver.Chrome()
# URL for data download
# Accessing the website
driver.get(url)
# Locating and clicking the download button
button = driver.find_element(By.ID, "fileRequest")
button.click()
# Loading the data into pandas
my_data = pd.read_csv('DIX.csv')
# Selecting relevant columns
selected_columns = ['price', 'gex']
my_data = my_data[selected_columns]
my_data['gex'] = my_data['gex'].shift(34)
my_data = my_data.dropna()
my_data = np.array(my_data)
plt.plot(my_data[:, 1], label='GEX')
plt.legend()
plt.grid()
my_data = pd.DataFrame(my_data)
my_data = my_data.diff()
my_data = my_data.dropna()
my_data = np.array(my_data)
def data_preprocessing(data, train_test_split):
# Splitting data into training and testing sets
split_index = int(train_test_split * len(data))
x_train = data[:split_index, 1]
y_train = data[:split_index, 0]
x_test = data[split_index:, 1]
y_test = data[split_index:, 0]
return x_train, y_train, x_test, y_test
x_train, y_train, x_test, y_test = data_preprocessing(my_data, 0.80)
model = RandomForestRegressor(max_depth=50, random_state=0)
x_train = np.reshape(x_train, (-1, 1))
x_test = np.reshape(x_test, (-1, 1))
model.fit(x_train, y_train)
y_pred_rf = model.predict(x_test)
same_sign_count_rf = np.sum(np.sign(y_pred_rf) == np.sign(y_test)) / len(y_test) * 100
print('Hit Ratio RF = ', same_sign_count_rf, '%')
plt.plot(y_pred_rf[-100:], label='Predicted Data', linestyle='--', marker='.', color='blue')
plt.plot(y_test[-100:], label='True Data', marker='.', alpha=0.7, color='red')
plt.legend()
plt.grid()
plt.axhline(y=0, color='black', linestyle='--')
The following figure compares the predicted values against the actual data.
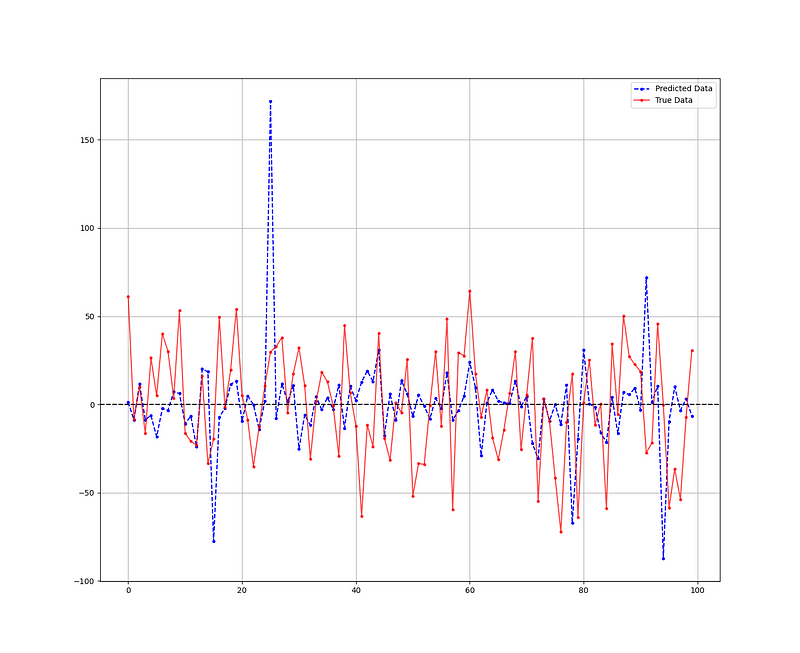
Evaluation of Algorithm Performance
The accuracy of the model is assessed through the hit ratio:
Hit Ratio RF = 57.40%
This indicates that the algorithm successfully predicts whether the S&P 500 will finish in positive or negative territory 57.40% of the time, which is a solid performance. Further improvements could involve adding more input features and optimizing the algorithm's hyperparameters.