Olympiad Techniques: Understanding AM-GM Inequality

As an author dedicated to problem-solving, I've decided to launch a series where I share various concepts and strategies for tackling challenges effectively. One of the most compelling aspects of competitions and Olympiads is that, even with the right techniques at hand, a problem can still be exceptionally tough. Familiarity with common problem types can be beneficial, but it's crucial to remember that there are often multiple solutions available, each offering unique insights. Today, we will delve into one of the most renowned inequalities: the Arithmetic Mean-Geometric Mean (AM-GM) Inequality.

First, let's clarify what it states.

In essence, the arithmetic mean is always greater than or equal to the geometric mean for non-negative numbers. While there are numerous proofs for this inequality, we won’t dive into them here. Those curious can explore various proofs online or even try proving it themselves.

At first glance, this inequality may appear to lack strength, yet it can be instrumental in solving problems that might otherwise seem insurmountable. Here’s a classic example:

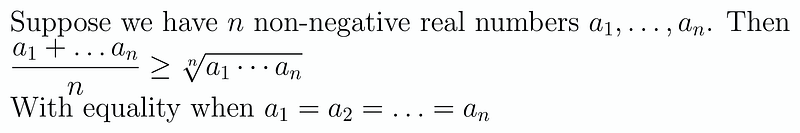
This problem is most conveniently tackled using AM-GM. Although one might attempt to manipulate ((a+b+c)^2), it wouldn’t be as straightforward as applying our inequality. Initially, the use of AM-GM might seem perplexing; simply inserting (a^2), (b^2), and (c^2) or the terms on the right won't yield useful results. So, what should we do instead? What if we applied AM-GM multiple times, focusing on pairs of terms? We can derive the following:

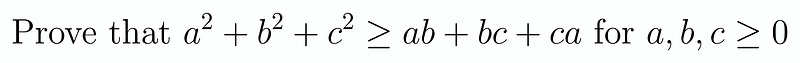
Continuing this cyclically with (b^2), (c^2) and then (c^2), (a^2) gives us three valid inequalities:

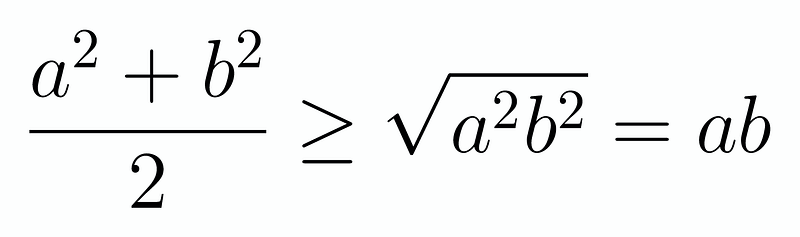
By summing these inequalities, we arrive at the inequality we set out to prove, thus completing our task. However, applying the inequality isn’t always straightforward, as demonstrated above. In some cases, it is simply a matter of direct application, as shown in my previous post.

Next, we introduce the weighted AM-GM inequality. Interestingly, we can introduce flexibility into our exponents by incorporating weights. This leads us to the weighted AM-GM inequality:

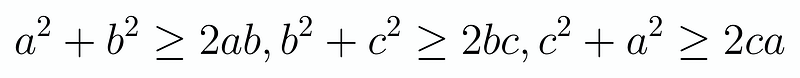
This formulation is quite similar, but now allows for arbitrary exponents and coefficients. While useful, it is less frequently encountered. We can illustrate this with an example from Brilliant:

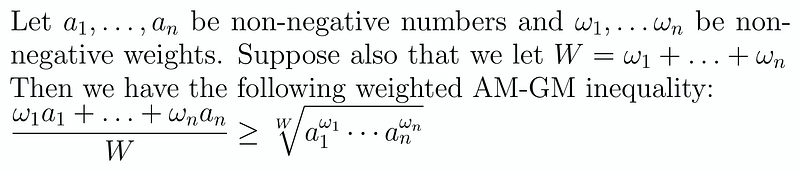
From the left side of the equality, we determine that our weights should be (3), (2), and (1). Consequently, dividing by a weighted product seems to be a wise choice. We find ourselves with:

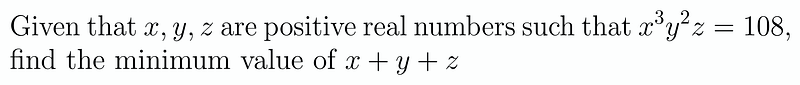
The rationale behind this division is that (3x/3 = x), and so on. Now, to establish the upper bound, we apply the weighted AM-GM to obtain:

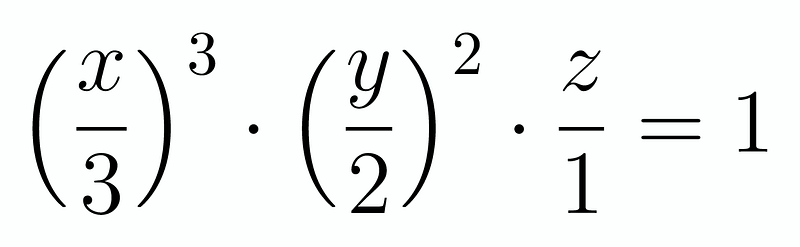
Thus, we conclude that the minimum value is precisely (6).

When is it most beneficial to use the weighted AM-GM inequality? Here are some typical scenarios:

• When the numbers in question are non-negative or positive.
• When the inequality represents a cyclic sum; this often leads to convenient cancellations.
• When the problem resembles any of the examples we've discussed; they often exhibit a similar structure.

Enjoyed this piece? Gained new insights? Your support would mean the world to me! If you’re interested in exploring a specific technique or would like me to walk through a particular problem, please feel free to reach out!

Chapter 2: Video Insights on Problem-Solving Techniques

For a deeper understanding of these concepts, check out the following video:

This video, titled "Two Techniques to Ace Math Olympiad Problems!", provides valuable insights on effective strategies for excelling in math competitions.