Optimizing Simulations Efficiently: Leveraging Scipy Interpolation
Written on
Understanding the Power of Interpolation
In the realm of scientific research and business analytics, interpolating experimental or simulation data is a common necessity. In my previous article, I detailed how to utilize Scipy for straightforward interpolation across one or multiple dimensions.
This video titled "Optimization with Python and SciPy: Unconstrained Optimization" delves into the core principles of optimization using Scipy. It provides insights into how simple interpolation methods can replace complex optimization algorithms, making it a practical choice for many scenarios.
Advantages of Using Scipy for Optimization
One significant advantage of employing Scipy's interpolation is that it provides an exact function that can be utilized for various purposes, including rapid optimization. This becomes particularly beneficial when experiments are expensive, as seen in fields like product design or drug testing. Given the high costs associated with each experiment, researchers must be strategic in their approach.
A practical methodology involves:
- Conducting a limited number of well-structured experiments (design of experiments knowledge is crucial here).
- Creating an interpolation function using linear, quadratic, or cubic splines.
- Evaluating the experimental results across a dense grid of points.
- Identifying the maximum or minimum values along with the corresponding input settings.
No complicated optimization algorithms or costly simulations are needed; a bit of design knowledge and interpolation routines can suffice.
The second video, "Modern Optimization Methods in Python | SciPy 2017 Tutorial | Michael McKerns," further explores modern optimization techniques within Python, emphasizing the efficiency and practicality of these methods.
Why Interpolation Works Well
Interpolation operates under the assumption that the underlying function is continuous and smooth. This assumption is illustrated in the following figure, which depicts the challenge of collecting numerous data points.
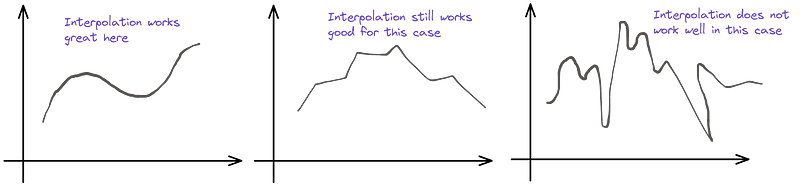
Most real-world continuous data problems exhibit enough smoothness, making them suitable for interpolation techniques. Therefore, a combination of physical simulations and interpolation can lead to effective optimization in various scenarios.
A Demonstration of Scipy's Interpolation Capabilities
For a practical example, let’s consider a simulation function that introduces a time delay while processing:
def complex_simulation(x):
"""
A nonlinear simulation function with some time delay
"""
time.sleep(0.1)
y = np.cos(-x**2/9.0) + np.sin(x/6)
return y
The run_experiments function executes this simulation over a defined range, collecting results:
def run_experiments(experiment_bounds, n=10):
results = []
low, high = experiment_bounds
domain = np.linspace(low, high, num=n, endpoint=True)
for i in domain:
y = complex_simulation(i)
results.append(y)
return (domain, results)
After running the simulation multiple times, we gather the data for analysis.
Interpolation and Optimization Techniques
Using Scipy for cubic interpolation produces a smoothly fitted curve and generates a function to derive intermediate results.
The code below demonstrates how to find the optimum point using exhaustive simulations:
def optimum_simulation(experiment_bounds, n=11):
"""
Using exhaustive simulations
"""
domain, results = np.array(run_experiments(experiment_bounds, n=n))
imax = np.argmax(results)
return (domain[imax])
This basic approach is slow due to the simulation delays. However, by employing the interpolated function, we can achieve faster results:
def optimum_interpolation(domain, init_results, n=101):
"""
Using interpolation
"""
low, high = domain.min(), domain.max()
ip_interpolated = np.linspace(low, high, num=n, endpoint=True)
f3 = interp1d(domain, init_results, kind='cubic')
results_interpolated = np.array(f3(ip_interpolated))
imax = np.argmax(results_interpolated)
return (ip_interpolated[imax])
With this method, computations are significantly quicker, often yielding more accurate results.
The Importance of Experimental Design
Proper design of experiments is critical for effective interpolation. Uniformly sampled experiment spaces generally yield the best outcomes. For example, using random sampling could lead to suboptimal results in interpolation.
In Summary
This article illustrates how leveraging simple interpolation methods and strategically chosen experimental points can facilitate rapid optimization. This technique is particularly beneficial for intricate simulations that exhibit smooth responses. Although demonstrated with simulated data in Python, the underlying principles apply to data sourced from various origins, including databases or APIs. Fields like semiconductor design and chemical process optimization stand to gain considerably from this approach.