Delving Into the Simple Sequence Challenge: A Unique Insight
Written on
Chapter 1: Introduction to the Sequence Problem
In this section, we will unravel an engaging sequences challenge from this year’s International Mathematical Olympiad (IMO), specifically Problem 3, which was the concluding problem on the first day. Typically, I wouldn’t consider tackling an IMO Problem 3, as they are designed for mathematicians far more advanced than myself. However, the straightforward nature of this problem intrigued me.
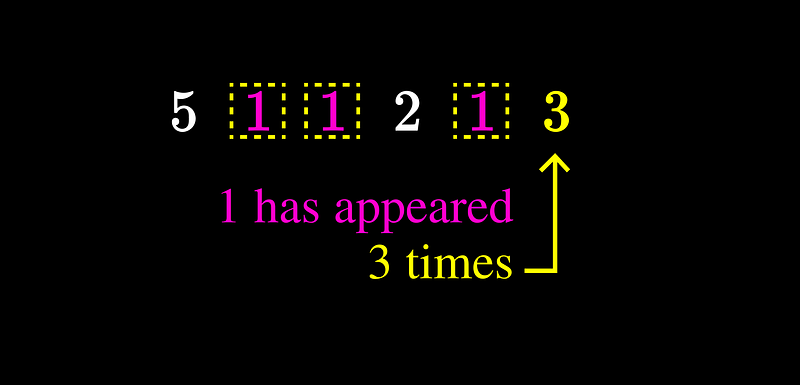
A fundamental aspect of the problem is that each term corresponds to the frequency of the preceding term in the list. Additionally, knowing that an Australian mathematician proposed this problem (my home country) only deepened my interest. I began experimenting with examples, first manually and then using a computer, to decipher why the sequence consistently becomes periodic. While the concept appeared evident and intuitive, proving it was quite challenging. After a week of contemplation, I’m prepared to elucidate the underlying mechanics.
Chapter 2: Experimenting with Sequences
To commence, let’s analyze the most basic scenario: where N = 1.
We can select any positive integer as the initial term; let’s choose 3. Consequently, the second term will be 1 (because 3 has been counted once). The third term will also be 1 (since 1 has been counted once), the fourth term will be 2 (as 1 has appeared twice), and so forth. Eventually, every second term cycles through {1, 2, 3, 1, 2, 3, …}, as illustrated in the animation below.

Let’s consider another example where N = 1, this time starting with an initial term of 5. The process takes a bit longer, but once again, we observe every second term repeating in a cycle {1, 2, 3, 4, 5, 1, 2, 3, 4, 5, …}.

Now, let’s increase the complexity to N = 2, starting with two distinct integers, say {3, 5}. I’ll skip the animation and directly show the first 50 terms.
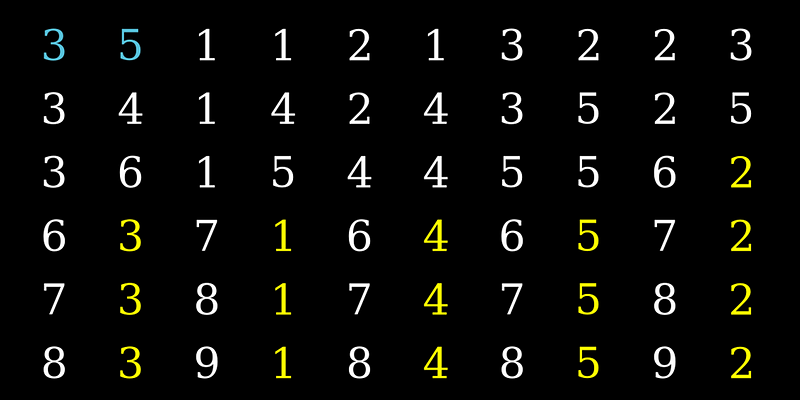
In this instance, the recurring sequence is {2, 3, 1, 4, 5}. You may have already formed some conclusions regarding the behavior of these sequences.
Section 2.1: Initial Observations
Here are some of my preliminary observations and conjectures:
- When a new number appears for the first time in the sequence, the next term is 1.
- A new number must eventually manifest, leading to the appearance of 1.
- Once 1 emerges, the subsequent term (its count) must increment by 1 each time. For instance, if 1 is followed by 7, the next 1 must be followed by 8.
- This pattern holds for all other numbers; if x appears followed by y, the next time x appears, it must be followed by (y + 1).
- Each time the count of 1 exceeds the maximum of the sequence, another 1 appears, suggesting that 1 will emerge indefinitely.
- The repeating subsequence appears to form a permutation of {1, 2, 3, …, n}, where n is the maximum value of the initial sequence.
However, this last observation is somewhat conjectural and, as it turns out, is incorrect!
Chapter 3: Understanding the Sequence Mechanics
Consider a counterexample where N = 7 and the initial terms are {7, 2, 2, 2, 2, 6, 2}.

In this case, the recurring sequence is simply {1, 2, 1, 2, 1, 2, …}.
Section 3.1: Analyzing the Sequence Dynamics
It’s evident from the earlier observations that 1 must be included in the repeating subsequence. In all previous examples, the recurring subsequence is a permutation of {1, 2, …, n}, where n is equal to or less than the maximum of the initial sequence. Does this always hold true?
For instance, can an initial sequence with a maximum of 7 lead to a repeating subsequence that includes an 8?
The answer lies in how an 8 could achieve a count of 8. Since it wasn’t in the initial sequence, the only way for 8 to appear in the sequence is as the count of another number. However, even if 1, 2, 3, 4, 5, 6, and 7 all appeared 8 times, 8 would only reach a count of 7.
In general, for any number greater than the maximum of the initial sequence, the condition for any k > m to achieve a count of k is that there must already be another j > m that has reached a count of j. This does not hold true initially, so no k > m can reach a count of k.
At this point, we’re making substantial progress!
The first video titled "Simple Sequence Stumps the World's Best! (IMO 2024 Problem 3)" dives into the mechanics of this fascinating problem, providing a visual explanation of its intricacies.
Section 3.2: Visualizing the Sequence through Histograms
Why must the repeating subsequence be a permutation of {1, 2, …, n}? Why can’t it be something like {1, 3, 1, 3, 1, 3, …}?
To address this, let’s utilize an x-y coordinate system, where the x-axis denotes each integer and the y-axis represents counts, resembling a histogram. We begin with a zero for every term in the initial sequence, then place each a(n) at the x-value of a(n+1). We stack it above any other numbers sharing the same x-value, meaning the y-value signifies the count of a(n+1).
Initially, the animation may appear to depict numbers randomly appearing on the x-y plane, but it serves a crucial purpose! The diagram below clarifies the placement of the first three terms {5, 1, 1} added to the initial sequence {3, 5}.
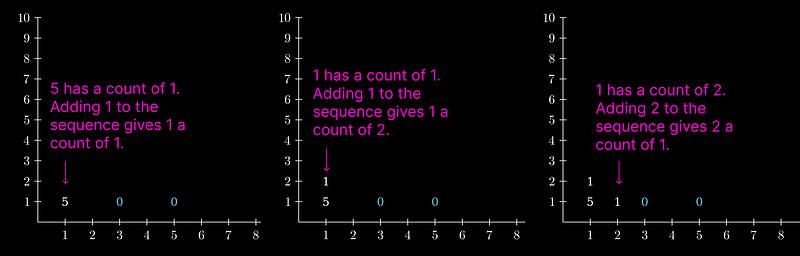
Let’s employ the histogram representation to illustrate why the repeating subsequence cannot be {1, 3, 1, 3, 1, 3, …} or any arrangement other than a permutation of {1, 2, …, n}.
Recall that the repeating subsequence must only include smaller numbers, which are less than the maximum of the initial sequence. As these numbers recur, their counts rise, introducing new larger numbers into the sequence. Yet, each new larger number must appear once before it can appear twice, and must appear x times before it can appear (x + 1) times.

If a repeating subsequence like {1, 3, 1, 3,…} were to exist, it would require each new large number to appear three times before having appeared twice, which creates a contradiction.
This leads to the conclusion that no integer can be omitted in the repeating subsequence, thereby mandating that it must be a permutation of {1, 2, …, n} for some n, which is less than or equal to the maximum of the initial subsequence.
Section 3.3: The Key Observation
You may have observed from the histogram representation that each column of yellow numbers is identical.

This will be a crucial observation for my proof. However, note that the arrangement of numbers in each column doesn’t directly correlate with the order of the repeating subsequence. In the example depicted, the repeating subsequence is {2, 3, 1, 4, 5} (as shown in the earlier example).
But the positioning of each number within the columns allows us to derive the repeating subsequence. Since the y-value of each number in the histogram indicates the count of the next term, let’s examine the column above the 10 for instance. Starting from the bottom:
- The 3 in the first row implies the sequence must include {3, 10, 1}
- The 5 in the second row implies the sequence must include {5, 10, 2}
- The 2 in the third row implies the sequence must include {2, 10, 3}
- The 1 in the fourth row implies the sequence must include {1, 10, 4}
- The 4 in the fifth row implies the sequence must include {4, 10, 5}
Assuming (which we will prove below) that after a certain point, this order must remain consistent for each column, we can deduce that:
- The next small number following 3 is 1,
- The next small number following 1 is 4,
- The next small number following 4 is 5,
- The next small number following 5 is 2,
- The next small number following 2 is 3.
This leads us to the repeating subsequence {2, 3, 1, 4, 5}, as anticipated.
Chapter 4: Proof of the Sequence Behavior
Let’s define any numbers that repeat infinitely as repeating numbers and any numbers larger than the maximum of the initial sequence as large numbers.
As previously explained, at least one repeating number (1) must exist because 1 is added whenever a new number is introduced. Moreover, no number can be both repeating and large, as a large number cannot reach a substantial count.
Eventually, all repeating numbers will have counts that are large numbers. Consider the point in the sequence where all repeating numbers have large counts, and a new large number (let’s call it X) has just been added for the first time.

I will demonstrate that the first repeating number to reach a count of X will also be the first to achieve a count of (X + 1), (X + 2), … and all numbers beyond X. Thus, this repeating number will maintain its position at the forefront of each column. The second number to reach a count of X will persist in the second position, and so forth, ensuring that the order of numbers in each column remains unchanged.
Let p be the first repeating number to attain a count of X. We must consider if another repeating number, say q, could reach a count of (X + 1) before p.

For this to occur, two large numbers must both achieve a count of q before p reaches (X + 1). Given that we are well into the sequence at this point where all repeating numbers have large counts, repeating numbers can only emerge as counts of large numbers.
However, two large numbers cannot have equal counts without a new large number being added between them. Proving this lemma is the most challenging aspect of my proof, but I believe it can be achieved.
Lemma: Two large numbers cannot reach an equal count without a new large number being added between them.
Proof: Counts must increment by 1 each time a number appears. If an x appears followed by a y, the next time x appears, it must be followed by (y + 1). In the histogram representation, this implies that a number can only appear in a specific column if it appears in the column directly to its left.
Consequently, a large number cannot achieve a count exceeding that of any number below it. Thus, if two large numbers attain equal counts, it must be the case that two consecutive large numbers, say Y and (Y + 1), have equal counts.
To establish that Y and (Y + 1) cannot both reach equal counts without a new large number being added between them, we consider the last number (denote it as x) that achieved a count of Y must also reach a count of (Y + 1). This necessitates that two large numbers must reach an equal count, with no new large number added in between.

However, when the first large number was introduced with a count of 1, if another larger number was added to its right with an equal count of 1, this would result in the sequence {1, X+1, 1, X+2, 1, X+3, …}, which has a repeating subsequence {1, 1, 1, …}.
Thus, it’s impossible for two consecutive numbers to reach equal counts without a new large number being introduced between them.
With this lemma established, we can conclude that the first repeating number to achieve a count of X will also be the first to reach counts of (X + 1), (X + 2), and so forth, implying that the n’th number to reach a count of X must also be the n’th to reach (X + 1).
Each of the n repeating numbers must maintain their order in subsequent columns, which leads to a unique mapping that results in a repeating subsequence.

Thank you for your patience throughout this explanation. I hope this clarifies the problem for you, and that you found it enjoyable. If you notice any errors or have any feedback, please don’t hesitate to share in the comments.
The official IMO 2024 solutions include two alternative proofs, both of which are quite different (and certainly more rigorous) than the one presented here.