Understanding Induction for Summation Evaluation
Written on
Chapter 1: The Importance of Summation
Summation plays a vital role in discrete mathematics and calculus. Those who have delved into calculus or computer science are likely familiar with expressions involving sums.

In theory, any sum can be computed using a computer with a simple loop. However, in practical scenarios—especially when dealing with millions of terms—adding each term individually can become tedious and inefficient. In such cases, it is beneficial to find a closed-form expression that allows for the computation of a sum without sequentially adding each term. A straightforward example of this is the arithmetic sum:
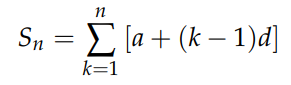
This sum resolves to:
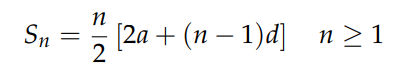
As seen, the outcome is determined solely by the constants a, d, and n. How do we derive such results? This article will explore various methods utilizing mathematical induction.
Section 1.1: Key Properties of Sums
Before diving into examples, it's essential to understand some fundamental properties of sums. First is the shifting index law:
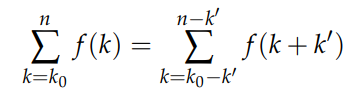
This law states that if we shift both the starting and ending indices by an integer amount -k, then the function f(k) must also be adjusted by +k. Conversely, shifting the indices by +k results in a -k adjustment to f(k).
The second principle is known as the permutation law, which indicates that:
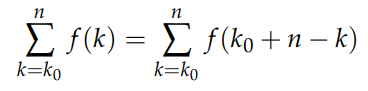
Upon closer inspection, we can keep the same indices but change the function f(k) by adjusting the sign on k, adding the initial and final indices to the argument. This process mirrors adding numbers in reverse order, yielding the same result.
Subsection 1.1.1: Understanding Arithmetic Series
Returning to the earlier example of summing an arithmetic series, the terms can be expressed as:
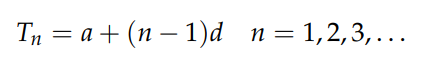
Here, a, n, and d are constants defining the sequence's boundaries. The sum of this sequence up to n terms is calculated as follows:
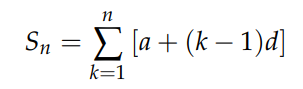
By applying the permutation law, we can rewrite it as:
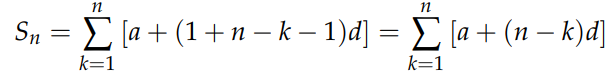
Both expressions are equivalent, as can be shown by expanding the terms. Adding both expressions results in:
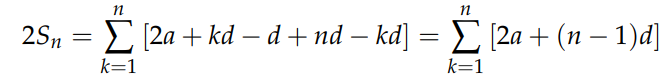
Since the expression in brackets is independent of the index k, we can factor it out, leading to:
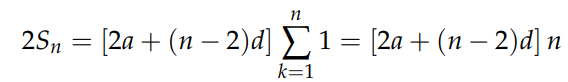
Rearranging provides the desired result:
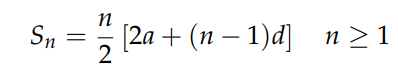
Chapter 2: Direct Induction Method
Consider a general sum expressed as:
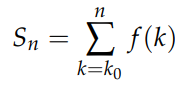
The expression for n+1 can be represented as:
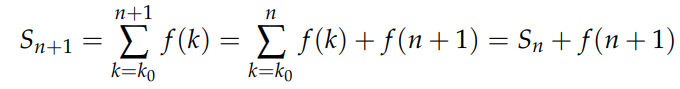
By extracting the last term of the sum, this can be seen as similar to extracting the first term:
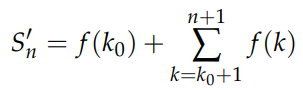
Both representations are equivalent, allowing us to write:
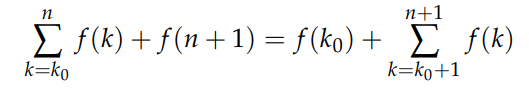
We can express the right-hand sum in the same format as the left by shifting the index by -1, resulting in:
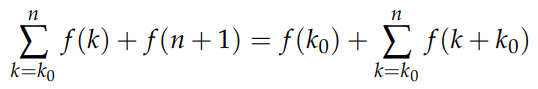
Upon rearranging, we find:
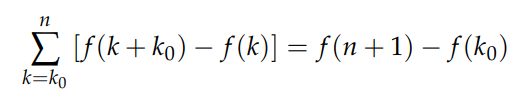
Thus, the original sum S can be evaluated as long as this final expression simplifies to contain S.
The first video titled "Using induction to prove summation closed form - Discrete Math for Computer Science" provides insights on how induction can be leveraged to establish closed forms for sums.
Example 1
To illustrate, consider the sum:
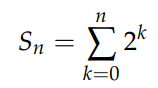
And the expression for n+1:
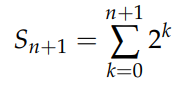
Extracting the last term gives us:
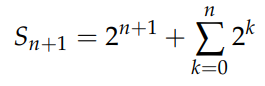
Extracting the first term results in:
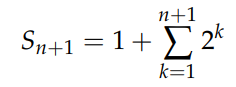
Writing the equality:
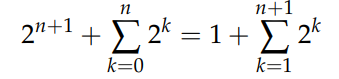
Shifting the index on the right-hand side:
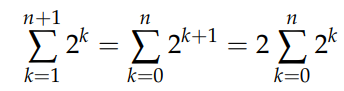
Allows us to express:
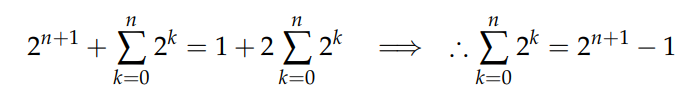
Example 2
Next, consider the sum:
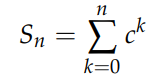
For any arbitrary number c, we follow the same procedure:
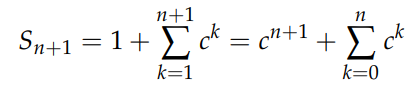
Then shift indices on the right:
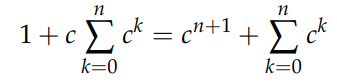
Rearranging yields:
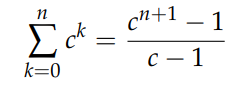
Note that this method may not be applicable to many sums; it depends on the function f(k).
Chapter 3: Indirect Induction Method
In particular cases, we can utilize an indirect method when direct induction fails. For instance, consider the sum:
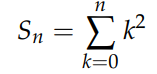
Following our usual method gives:
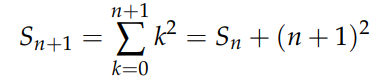
And:
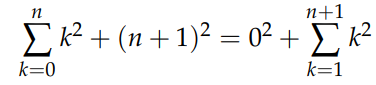
Lowering the index on the right yields:
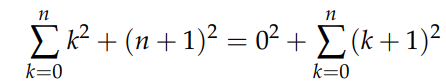
Expanding the new series results in:
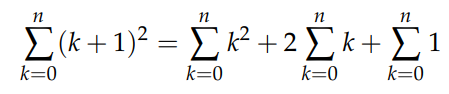
This yields:
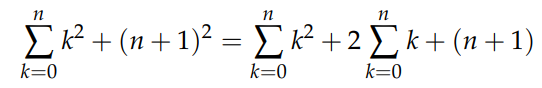
However, this expression indicates that the original sum S cancels out on both sides, simplifying to:
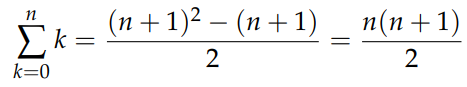
This case represents a special instance of the arithmetic sum. To resolve the sum of squared integers, we consider if the sum of k² gives the sum of k, perhaps the sum of k³ will yield the sum of k²? Let's explore that. Consider the new sum:
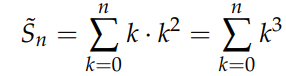
Applying the perturbation method, we express:
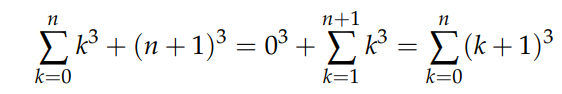
Expanding the right side:
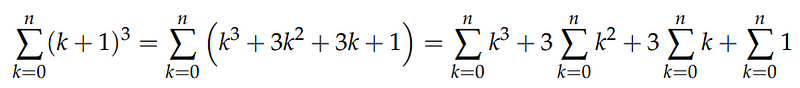
Results in:
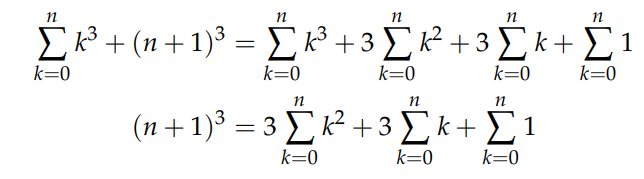
The k³ sum cancels out on both sides, leading to:
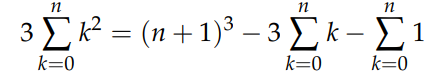
Rearranging gives:
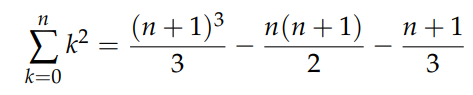
Or alternatively:
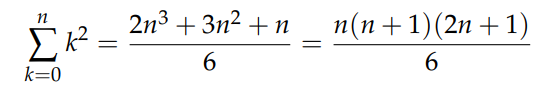
This is indeed the desired outcome for k². The elegance of this method lies in its applicability to higher powers of k. To derive the sum of k³, we begin with:
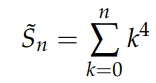
Then, by expanding using the perturbation law:
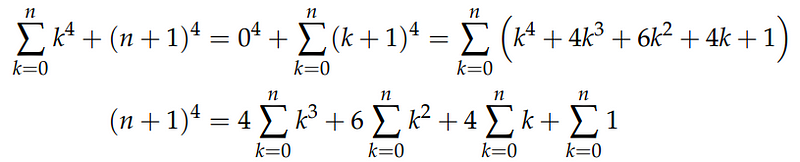
Canceling the k terms yields the desired sum:
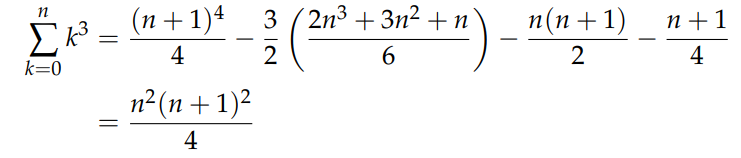
The second video titled "Induction with Sigma Notation (1 of 4: Basic example)" further elaborates on using induction with sigma notation, providing foundational understanding for summation techniques.