Section 1.1: An Overview of Normal Distributions

Normal distributions are characterized by their symmetrical shape and fair nature, akin to a character like Harry Potter.

When discussing phenomena described as 'normally distributed,' many visualize a bell curve where the average sits at the center, with values tapering off symmetrically on either side.

A normal distribution is defined by two parameters: the mean (µ) and the standard deviation (σ). The mean indicates the center, while the standard deviation measures the spread from this center.

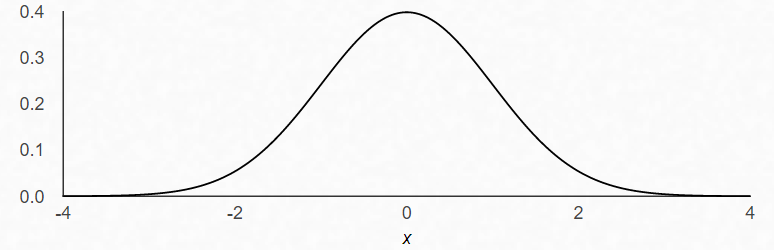
Normal distributions can be observed in various contexts, such as IQ scores, height, and exam results. Their predictable nature makes them easier to manage. For instance, a tailor serving clients with heights that follow a normal distribution would only need to account for those within three standard deviations from the mean, effectively covering about 99.7% of potential customers.

To better understand normal distributions, it’s vital to consider the central limit theorem. This theorem states that the sum of N random variables, where N is typically greater than 20, will approximate a normal distribution, provided the variables are independent and have finite variance.

As an example, consider human height, which is influenced by both genetics and environmental factors. Around 180 genes are known to affect height, and if each gene operates independently, the resulting heights in a population will tend to be normally distributed.

By now, you should have a foundational understanding of normal distributions, enabling you to identify situations where this distribution might apply.

Section 1.2: The Nature of Long-Tailed Distributions

In contrast, long-tailed distributions can be likened to unpredictable characters, such as the Hulk.

These distributions, also known as power law or Pareto distributions, are less intuitive than normal distributions, making them harder to identify. However, they are prevalent in nature, emerging in contexts such as wealth distribution, book sales, forest fire sizes, and earthquake magnitudes.

Long-tailed distributions are defined by power law relationships, where p(x) can be expressed over an interval [min, ∞). The exponent (α) in this expression (> 1) determines the length of the tail.

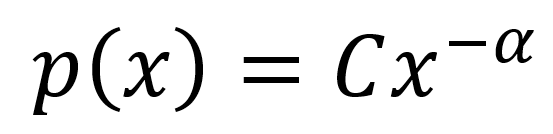
For those unfamiliar with these distributions, they may seem inherently unfair. Unlike normal distributions, long-tailed phenomena are not centered around a midpoint; they are asymmetrical, with extreme events being rare yet capable of causing immense impacts.

Section 1.3: How Long-Tailed Distributions Manifest

Two primary models explain the emergence of long-tailed distributions:

1. Preferential Attachment: In a network of interconnected nodes, more popular nodes are likely to attract even more connections. This phenomenon can be observed in social media, where accounts with many followers tend to gain even more.
2. Self-Organized Criticality: In this model, consider an empty grid where random sites grow trees. If lightning strikes a tree, it may start a fire that spreads to connected trees. Most fires are small, but as the forest densifies, the potential for a massive fire increases.

To illustrate this concept, here’s a simulation of self-organized criticality in action, particularly within the context of forest fires.

Section 1.4: The Importance of Recognizing Long-Tailed Distributions

Understanding long-tailed distributions is crucial, especially when considering events such as earthquakes, which often follow a power law distribution with an exponent of approximately 2.

For instance, the devastating 2011 earthquake in Honshu, Japan, had dire consequences, and while such significant events are rare, their potential impact is profound. An earthquake of this magnitude, occurring roughly once in a million days, poses a significant risk over a century.

The potential for catastrophic outcomes highlights the necessity of awareness and preparedness for such rare occurrences. Failure to recognize long-tailed phenomena can lead to inadequate responses from governments during extreme events, resulting in severe destruction.

Nassim Nicholas Taleb refers to these unpredictable yet impactful events as "Black Swan Events." Here are some notable examples of such occurrences:

• The 2004 Indian Ocean tsunami
• The 2008 global financial crisis
• The COVID-19 pandemic