Understanding Why Triangle Angles Sum to 180° and Beyond

Chapter 1: The Foundations of Euclidean Geometry

To delve into the reasons behind the total internal angle of a triangle being 180°, and why it totals 540° for a pentagon, we must revisit the time of Euclid and his seminal work, the Elements. The first book outlines five foundational postulates, but we will concentrate on the fifth, known as the Parallel Postulate:

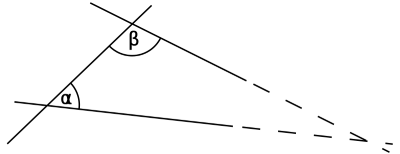
This postulate states that if two lines intersect a third line in such a way that the sum of the angles on one side is less than two right angles, those two lines will eventually intersect if extended far enough. Modern interpretations suggest that if two lines are parallel and intersect a third line, the sum of the angles on either side will equal 180°.

This remarkable number, 180, will help us answer our earlier questions about angles in triangles and polygons.

Total Internal Angle of a Triangle

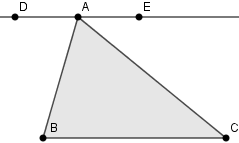
Consider triangle ABC depicted in the figure above. Draw a line ( l ) through point A that is parallel to side BC. Let points D and E be located on this line, with D on the left of A and E on the right. According to the postulate, we can conclude that ( angle ABC + angle BAE = 180° ) and ( angle BCA + angle CAD = angle CAE + 180° ). Thus, we derive that:

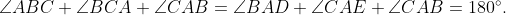
It follows that the total internal angle of a triangle is indeed 180°.

Total Internal Angle of a Convex n-gon

A convex n-gon can always be divided into ( n - 2 ) triangles through a process called triangulation. To illustrate, if we have a hexagon (n = 6), one can choose a vertex and connect it with diagonals to all other vertices, as shown in the following figure:

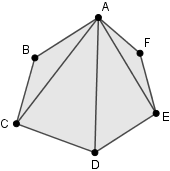
Key points to note about this triangulation include:

All drawn segments remain within the n-gon, as it is convex.
The resulting triangles do not overlap.
Each vertex of the triangles corresponds to a vertex of the n-gon.

From these observations, we can conclude that each internal angle of the triangles contributes uniquely to the overall internal angle of the n-gon. Since there are ( n - 2 ) triangles and each contributes a total of 180°:

Theorem 1.3

A convex n-gon has a total internal angle of ( (n - 2) times 180° ).

Endnote

Now that we understand the total internal angle of a pentagon is 540°, we can also determine that a dodecagon's total internal angle is 1800°, and so on. Referring back to Figure 1.3, angles ( angle ABC ) and ( angle BAE ) are known as co-interior angles, while ( angle ABC ) and ( angle BAD ) are termed alternate angles.

Thanks for reading. Cheers!