Unlocking the Secrets of Movement: Math's Role in Modeling
Written on
Chapter 1: The Intersection of Mathematics and Movement
Mathematics plays a pivotal role in understanding movement, particularly through classical mechanics, a branch of applied mathematics that I find incredibly fulfilling. The process of transforming particle motion scenarios into mathematical equations reveals the inherent beauty of these concepts.
To demonstrate this, I will share a problem I recently explored, which applies mathematics to analyze the outcomes of collisions involving multiple particles. This analysis establishes a mathematical framework for the ensuing events, leading to conclusions that, while intuitive, are fascinating to validate through mathematical reasoning.
Section 1.1: Visualizing the Collision Scenario
In tackling such problems, it’s not uncommon for them to appear daunting when presented abstractly. However, a simple diagram can clarify the situation we're examining. Below is a rough sketch depicting the scenario before the collision.

The key concept here is that kinetic energy remains conserved throughout the collision process. A collision where kinetic energy is not lost is termed a perfectly elastic collision. While this may be somewhat unrealistic—since marbles typically produce sound upon colliding, indicating some energy loss—it serves our purpose for analysis.
Section 1.2: Establishing Key Definitions
To begin our analysis effectively, we need to adopt clear and manageable terminology. Initially, we recognize that before the collision, only particle A is in motion, traveling with a velocity denoted as u. Post-collision, the velocities of the particles become unknown, so we'll label them as v₁, v₂, v₃, etc.
From our understanding of isolated systems, we have two fundamental principles: momentum conservation and kinetic energy conservation. The total momentum prior to the collision equates to the total momentum afterward, mathematically expressed as follows:

Similarly, the total kinetic energy before the collision matches that after the event:
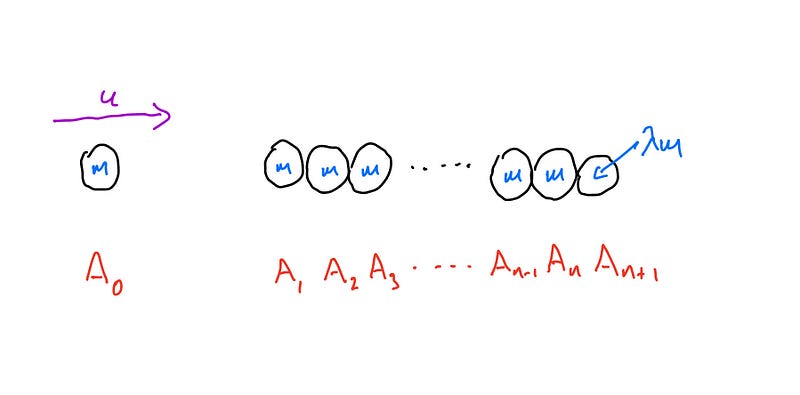
If we assume that only the last two particles move post-collision, we can simplify our equations accordingly.
Chapter 2: Analyzing Post-Collision Dynamics
In the first video, "The Power of Mathematical Modelling - Nira Chamberlain FORS," the speaker discusses how mathematical modeling can be used to analyze physical phenomena, including collisions.
Continuing with our scenario, we find ourselves faced with two equations that can be simplified further:
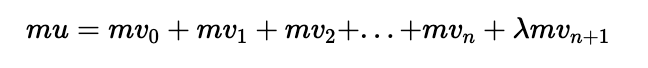
By factoring out constants from our equations, we can reduce them to a simpler pair, allowing us to substitute values effectively.
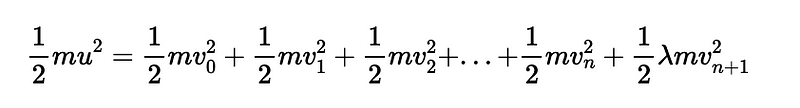
As we delve deeper into our analysis, we reach the conclusion that if the last particle is lighter than the others, it must indeed possess a positive velocity.
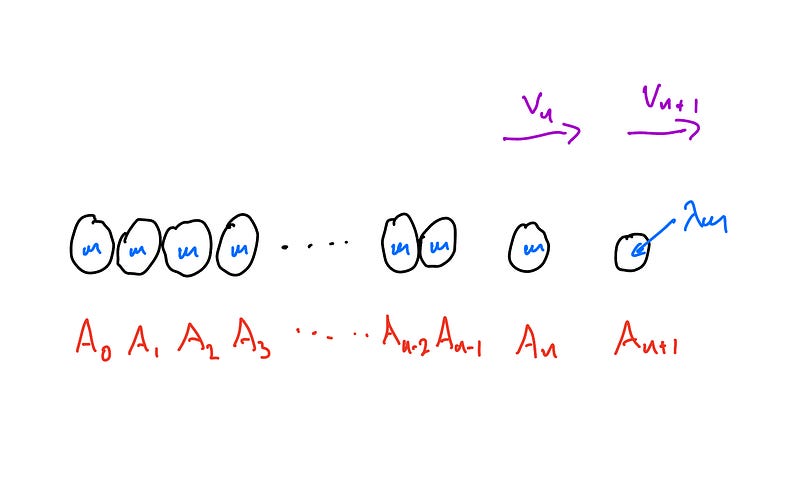
Part (ii): Exploring Heavier Last Particles
Next, we explore the scenario where the last particle is heavier than the preceding ones. Using a similar approach, we can derive new simultaneous equations:
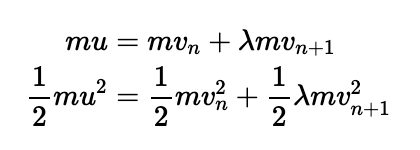
Assuming the last marble's weight exceeds that of the others leads us to a contradiction, illustrating that such a scenario cannot occur.
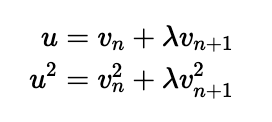
Part (iii): Generalizing the Findings
Finally, we can generalize our findings. For any two-particle interaction, the rightmost particle must be one that moves forward, confirming it must have a positive velocity. Therefore, if we extend our previous analysis, we conclude:
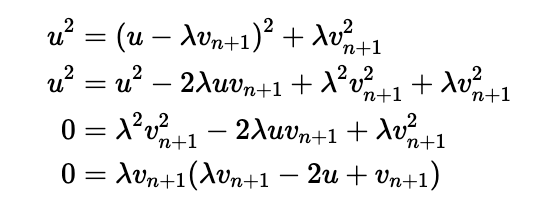
In summary, this investigation into particle collisions reveals fundamental truths about motion and the conservation laws that govern it.
The second video, "The Five Step Method - Math Modelling | Lecture 1," presents a structured approach to mathematical modeling, offering valuable insights for those interested in this field.
What are your thoughts on this mathematical exploration? I welcome your comments and feedback!