Understanding the Relationship

Imagine we wish to draw a line with a positive slope, m, that passes through either the left or right focus of a wide ellipse. Is there a connection between the slope m, the ellipse constants a and b, and d, which represents the distance between the intersection points of the ellipse and the line?

Indeed, there is! Although deriving this relationship mathematically involves quite a bit of complexity (which is elaborated in my math book linked at the end), we will forgo the detailed derivation in this discussion and simply present the equation.

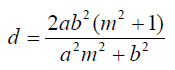
Take a moment to examine this equation. Notice how both a, b, and m appear in the numerator and denominator. There's also an a raised to the first power in the numerator, while the other five variables are squared. This equation is truly fascinating!

Now, let's get to work! I encourage you to solve this equation for a², b², and m. Remember, math is an active pursuit, not a passive one; I aim to enhance your mathematical skills through this publication (Intro to Math). So, please engage with this equation.

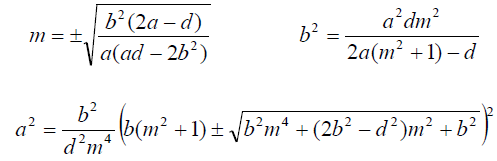
If you've tackled this challenge and derived the correct results, congratulations!

Next, I invite you to try problem #6 from my book in this chapter:

I utilized Wolfram Alpha to find the coordinates of the intersection points. You can input these coordinates into the distance formula and check if your results for both parts a and b match.

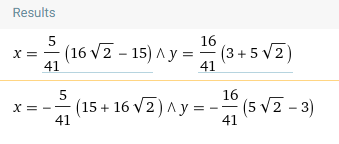
Here is the illustration generated by Wolfram Alpha for this problem.

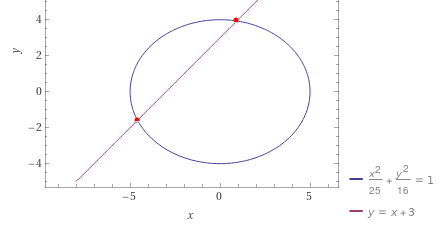
As a rough estimate, the diagram appears to indicate a distance of about 8 or 9 units. If your answers align and are approximately 8 or 9 units, then you've successfully completed the task. Well done!

Chapter 2: Video Insights

Explore how the relationship between a, b, and c applies to ellipses in this informative video.

Discover the beautiful proof that slicing a cone results in an ellipse in this engaging video.