Understanding Patterns in Sequences

It often happens that we intuitively feel a sequence may exhibit a specific pattern. To validate these suspicions, mathematicians utilize a powerful technique known as mathematical induction.

In this article, we will tackle a thought-provoking problem sourced from the TMUA, an assessment designed for prospective computer science students at the University of Cambridge. While many may quickly arrive at the value of u_(1000), the real challenge lies in demonstrating its accuracy.

To assist you, consider this clue: try evaluating a few integrals.

Pause here, grab your pen and paper, and see if you can solve it before continuing for the solution!

Calculating the Terms

We start with the initial condition u0 = 1, applying the established rule to compute u1.

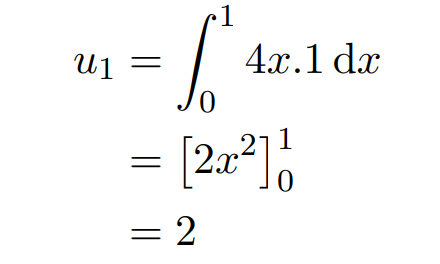
Thus, we find u1 = 2. Next, we can compute u2 using the value of u1.

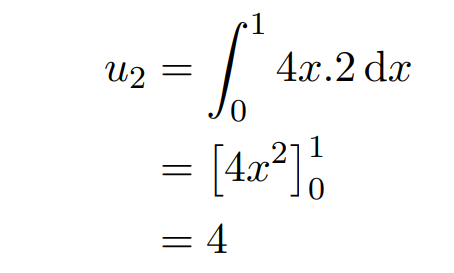
This leads us to u2 = 4. Continuing this process, we will now calculate u3 using u2.

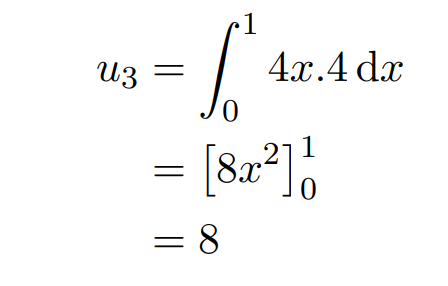
Do you notice a trend?

• u1 = 2¹
• u2 = 4 = 2²
• u3 = 8 = 2³

It appears that the general term un can be expressed as 2 raised to the power of n:

un = 2^n.

This holds true, leading us to the conclusion that:

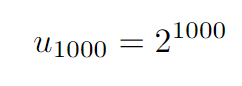
Exploring Mathematical Induction

The foundation of mathematical induction begins with verifying that the base case is accurate. In our scenario, we check if the rule is valid for n = 1:

n = 1

u1 = 2¹ = 2, confirming its truth for n = 1.

Now, let’s assume it holds true for n = k:

uk = 2^k.

This assumption is crucial as we will use it in our final step to demonstrate its validity for n = k + 1.

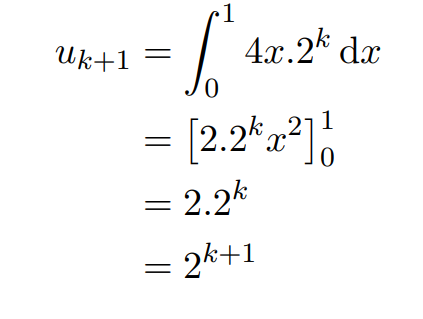
In the inductive step, we substitute uk = 2^k into our equation. After performing the necessary calculations, we arrive at:

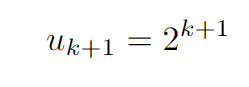
Thus, through the principle of induction, we have confirmed that un = 2^n for all n greater than or equal to 0!

Visualizing Induction

Mathematical induction can be likened to a sequence of dominoes falling; the first one tips over the second, which then causes the third to fall, and this continues indefinitely.

What was your approach to solving this problem? I’m curious to hear your thoughts in the comments below!

The first video titled "Cambridge University Entrance Math Problem" explores this math challenge in depth, providing insights and approaches to the problem.

In the second video, "Math Genius: Can You Prove Which Is Greater Between..." we delve into comparative proofs, enhancing our understanding of mathematical reasoning.

Thank you for engaging with this content. Don’t forget to show your appreciation if you found this article informative!

If you enjoyed this article, consider supporting my work. Your generosity fuels my writing and academic journey.

Happy solving!