# Understanding Electric Energy Flow in Wires and Beyond
Written on
Chapter 1: The Nature of Electric Energy
Electric energy possesses intriguing characteristics that set it apart from other energy forms. One notable advantage is its efficiency in being converted into mechanical energy with minimal loss and environmental impact.
From our educational experiences, we learn that electric current is essentially the movement of charged particles, predominantly electrons in conductive materials like metals. But can these electrons fully account for the energy that wires transmit? In this discussion, we will demonstrate a straightforward method to illustrate that the electric and magnetic fields surrounding the wires actually contain all the energy transferred from a power source to a device.
Section 1.1: A Practical Example with Coaxial Cables
To visualize how energy flows beyond the wires, let’s consider a coaxial cable as a prime example:
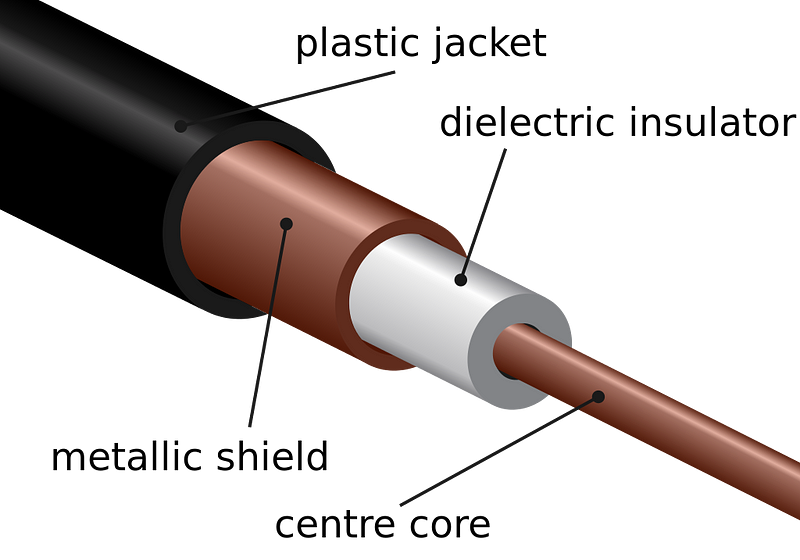
Source: wikimedia.org
For our analysis, we will focus on a segment of the cable that is one unit long. To simplify our calculations, we will assume a direct current flows between the central conductor and the metallic shield, with the cable's resistance approaching zero. We can posit that the central core is connected to the positive terminal while the metallic shield is connected to the negative terminal. For current to flow, a voltage V must exist between these two conductors, resulting in a stationary electric field E. The positive charge of the central wire causes vector E to direct from the core to the shield, resembling a cylindrical capacitor:
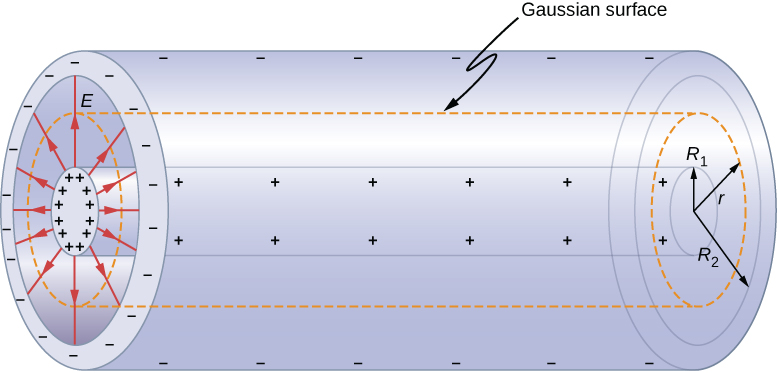
Source: mtstatic.com
The electric field between the conductors can be expressed as E=V/rln(R2/R1), where R1 and R2 are the radii of the inner and outer conductors, respectively. When a current I flows through the wire, it generates a magnetic field outside the conductor, which can be described by H=I/2?r.
Section 1.2: Utilizing the Poynting Vector
To quantify the energy transmitted by the electromagnetic field within the insulating medium, we employ the Poynting vector. This vector represents the energy passing through a unit area over time. Since electric and magnetic fields are orthogonal, calculating their cross product to find the Poynting vector is straightforward: S=EH=VI/2?r²ln(R2/R1). This vector aligns parallel to the cable, and its flux across the insulating cross-section is given by F=VI.
From our prior knowledge, the electric power consumed by a device, such as a microwave oven, is defined as P=VI, where V denotes voltage and I signifies the current required by the appliance. Therefore, it is evident that energy flows through the space surrounding the wires (in the insulator) as part of the electromagnetic field, moving from the source to the device.
Chapter 2: The Impact of Resistance
However, it is essential to acknowledge that resistance is not negligible. In reality, to supply sufficient energy to an electrical device, we must provide more power than the device’s nominal requirements. This discrepancy arises due to Joule heating within the conductor, where some electric energy is dissipated as heat. Consequently, the wire itself acts as a heating element, necessitating a nonzero electric field component directed along the wire. When resistance is present, the Poynting vector also has a component directed perpendicular to the wire, indicating that some electromagnetic energy indeed penetrates the metal conductor. This energy flowing through the wire corresponds precisely to the Joule heating effect.

Source: freepik.com
Section 2.1: The Role of Alternating Current
For alternating current (AC) at lower frequencies, the transmission of energy operates similarly. Each time the electric field reverses direction, the magnetic field also shifts, ensuring that the Poynting vector consistently indicates the path of energy transmission.
Section 2.2: Energy Storage in Electrons
Can electrons indeed store some energy? If they could, one might expect their inertia to influence resistance. For example, sharp bends in a wire might increase resistance, akin to water flowing through a twisted pipe. Nevertheless, our everyday observations confirm that resistance remains largely unaffected by such factors, indicating that the energy stored in charged particles is trivial compared to the energy held within the electromagnetic field.
If you wish to explore more articles on space and science topics, feel free to subscribe to our channel and engage with your questions, which I will address in future articles. Your support is invaluable; consider joining our community on Medium for just $5 a month to help us create even more enriching content.