Chapter 1: Introduction to Key Concepts

In the field of control engineering, we frequently encounter the terms noise, disturbance, and uncertainty. Are these concepts interchangeable? If not, what distinguishes them, and how do they impact our systems? These questions often arise, particularly among students in control engineering. This article aims to clarify these terms as succinctly as possible.

Section 1.1: What is Noise?

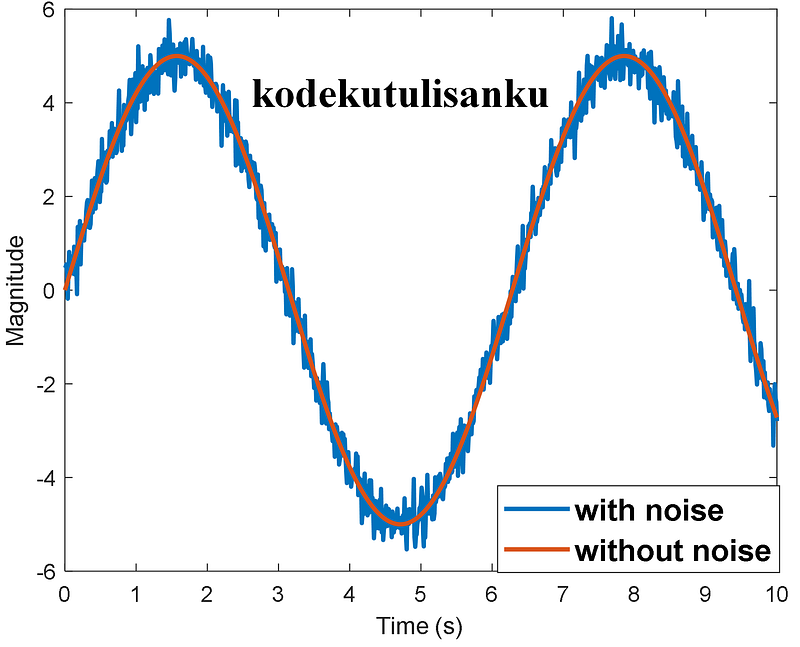
Noise is a term that many are familiar with, even outside of control engineering. In this domain, it is crucial to consider noise, especially when working with controllers that include a derivative term. For example, when utilizing a Proportional-Derivative (PD) controller, one often needs to implement additional measures, such as a low-pass filter, to mitigate the effects of noise on the controller's performance.

Typically, noise is characterized by high frequency, which is why low-pass filters are employed. Noise can originate from various sources, including sensor readings, connectors, cables, and environmental factors. Consequently, you may come across terms like measurement noise, output noise, and input noise. Each type of noise affects different aspects of the system; measurement noise appears in sensor readings, while input and output noise impact the system's input and output, respectively. For instance, connecting a microphone to a speaker may result in audible sounds from the speaker even without any input from the microphone, highlighting the presence of noise.

Different types of noise, such as white noise, pink noise, and brown noise, exist, but we will delve into these specific categories in future discussions. Can noise destabilize your system? The answer lies in the design of your controller. If it is overly sensitive to noise, the stability of the system may be compromised.

Chapter 2: Exploring Uncertainty

Uncertainty, often referred to as variation, represents the discrepancy between a real system and its mathematical model. For example, a car is inherently a complex nonlinear system, yet we may simplify it by assuming a linear model, which leads to inaccuracies in behavior prediction. Additionally, uncertainty can arise from manufacturing processes; for example, a manufacturer may produce a hundred vehicles that, while similar, are never exactly identical.

Another illustration involves the mathematical modeling of a truck trailer; the model will differ significantly depending on whether it is loaded or unloaded. If you have examples of uncertainty, feel free to share them in the comments. Control engineering students may also encounter the terms structured and unstructured uncertainty, particularly when studying robust control. Don’t worry if this sounds unfamiliar; it will become clearer with further study.

From this explanation, it is evident how significantly uncertainty can influence your system's behavior.

Section 2.1: Understanding Disturbance

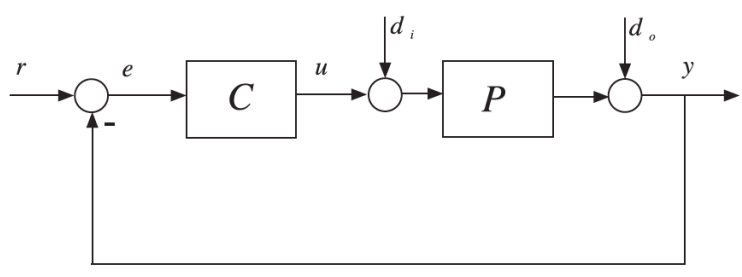
Disturbance refers to signals that negatively impact a system's output. If a disturbance originates within the system, it is classified as internal; conversely, external disturbances come from outside the system. This terminology frequently appears in conference papers, journals, and articles focused on control systems.

For instance, in autonomous vehicles, disturbances may include road bumps (external), inclines and declines (external), wind gusts (external), and inaccuracies in low-level controllers (internal). Input and output disturbances are also common terms; input disturbances can alter the system dynamics before they enter the plant, while output disturbances affect the signal as it exits the system.

Understanding disturbances is crucial for designing effective controllers, as they can indeed destabilize a system. Therefore, when developing a controller, one must consider the magnitude of potential disturbances to ensure stability.

Chapter 3: Further Exploration and Resources

If you have any feedback or believe any explanations here could be improved, please share your thoughts in the comments. I welcome constructive suggestions.

The first video titled "System Dynamics and Control: Module 26b - Uncertainty, Disturbances, and Noise" discusses the interrelations of these concepts, providing a deeper understanding of their impacts on control systems.

The second video, "A. Abbott: 'Noise and disturbance for qubit measurements: An information-theoretic characterisation'" offers a unique perspective on noise and disturbance in measurements, particularly in the context of quantum systems.