Understanding the Unique Role of 3 in Division
Written on
Chapter 1: The Significance of 3 as a Denominator
What makes the number 3 stand out when used as a denominator? It turns out that 3 has a unique property: if the sum of the digits in the numerator is divisible by 3, then the numerator itself is divisible by 3, resulting in a zero remainder.
For instance, to determine if 7215 is divisible by 3, we first add its digits: 7 + 2 + 1 + 5 = 15. Since 15 is divisible by 3, we can conclude that 7215 is also divisible by 3. A quick calculator check confirms that 7215 ÷ 3 = 2405, which indeed leaves no remainder.
Now, let’s explore this concept with the number 2. Take 7242; summing its digits gives us 7 + 2 + 4 + 2 = 15. While 15 is not divisible by 2, 7242 is (7242 ÷ 2 = 3621). Now what about 5? If we look at 6135, the digit sum is 6 + 1 + 2 + 5 = 14. Although 14 is not divisible by 5, 6135 is (6135 ÷ 5 = 1227). This suggests that 3 indeed has a special role here.
If you’re curious like I am, let’s delve deeper to understand why this is the case.
The Decimal Number System Explained
Before we explore the mystery of 3's unique property, it's essential to understand how the decimal number system operates. The rightmost digit (before the decimal point) represents the ones place, followed by the tens place, hundreds place, and so on. This understanding allows us to express larger numbers as the sum of their digits, each multiplied by its respective place value.
Here are a few examples for clarity:
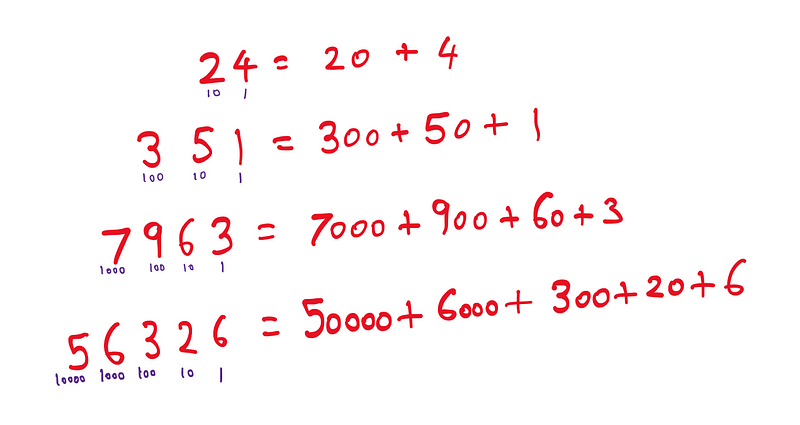
Why is 3 a Unique Denominator?
If a number’s digit sum is divisible by 3, then the entire number will also be divisible by 3. We can use our earlier review of the decimal system to clarify this. Consider the number 612. Assigning letters to each digit gives us a = 6, b = 1, and c = 2. We can express 612 as:
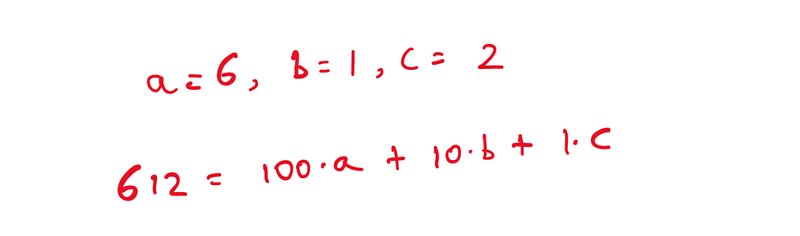
This can be rewritten as:
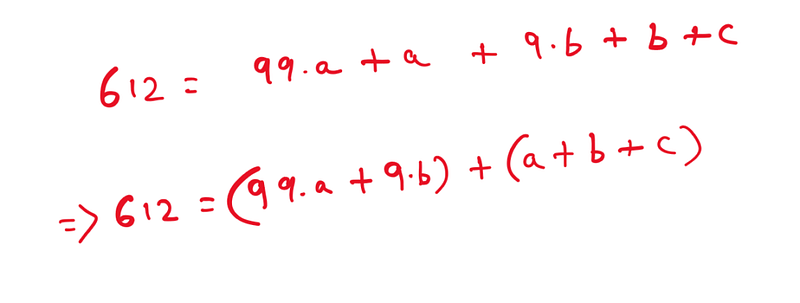
Clearly, (99*a + 9*b) is divisible by 3 since it includes 9 as a common factor. For the rest of the expression to be divisible by 3, (a + b + c) must also be divisible by 3. We can apply this method to larger numbers, and it will consistently lead us back to the (a + b + c) term needing to be divisible by 3. This is the underlying reason why if the sum of a number's digits is divisible by 3, the number itself is as well.
The Order of Digits Is Irrelevant
Having established that 612 is divisible by 3 (612 ÷ 3 = 204), we see that the order of the digits doesn’t affect this property. All permutations of the digits 6, 1, and 2, such as 612, 261, 126, 621, 216, and 162, will still be divisible by 3. This is an interesting sub-property worth noting.
Recursive Methods for Quick Mental Calculations
If you need to check a large number's divisibility by 3 without a calculator, the process we’ve discussed can also be applied recursively. In simpler terms, you can continually sum the digits until you reach a manageable number for mental calculation, which will still indicate whether the original number is divisible by 3. Here’s a practical example:
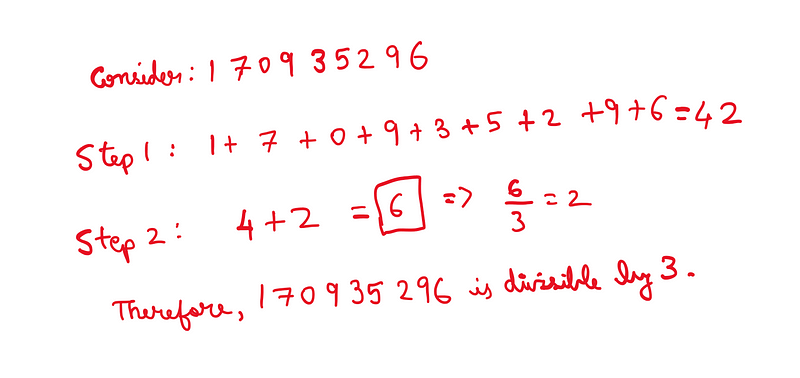
I hope you found this exploration both intriguing and informative. If you appreciate my work, consider giving a clap, following, or subscribing for more insights.
For further reading, you might enjoy: How To Use Mathematics To Choose A Life Partner? and Why Is A Number Raised To The Power Zero Equal To One?
The Decimal Number System in Action
This video, titled "Math Antics - Fractions Are Division," provides an engaging overview of fractions and division.
Dividing Fractions Made Easy
This video, "How to Divide Fractions Where the Numerator Is Smaller Than the Denominator: Division Tips," offers helpful tips for dividing fractions.