Chapter 1: Understanding Gauge Symmetries

In previous discussions, I have delved into the idea of symmetry within the realm of physics. A particularly accessible symmetry group is U(1), which is composed of complex numbers that maintain a unit length. The manifold linked to the U(1) group is the unit circle, classifying it as a Lie group, as locally it resembles one-dimensional Euclidean space. The most notable theories arising from a U(1) symmetry include electromagnetism and quantum electrodynamics. However, there are additional intriguing models within U(1) gauge theories worth exploring. The key requirement is that the Lagrangian associated with the gauge potential ( A ) must demonstrate some form of invariance, possibly necessitating the imposition of certain constraints.

The gauge transformations relevant to U(1) are described below. The vector ( A ) functions as a one-form, representing the gauge potential, while the wavefunction on the right transforms as if being multiplied by a phase factor.

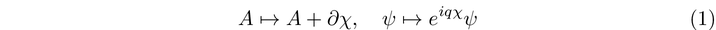
It’s important to remember that the electromagnetic tensor derives from the gauge potential by taking the exterior derivative, as shown below. This object is generally referred to as a ‘field strength’ tensor, and its significance extends beyond just electromagnetic theory.

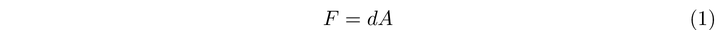
The gauge potential is a one-form, allowing it to be expressed as a linear combination of differential forms. In terms of components, we can illustrate the gauge potential as follows:

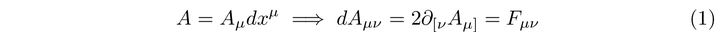
It can be easily shown that the electromagnetic tensor remains invariant under U(1) gauge transformations. Previously, I have covered the Lagrangian for electromagnetism, which leads to Maxwell’s equations. Nevertheless, this is not the only viable model. One of the most fascinating forms is the Chern-Simons term, characterized by a Lagrangian that depends on the gauge potential rather than the electromagnetic tensor. Chern-Simons forms are applicable in diverse fields, ranging from topological quantum field theory to condensed matter physics.

What is the structure of the Chern-Simons form?

To streamline our analysis, we will consider a two-dimensional spatial framework alongside one time dimension.

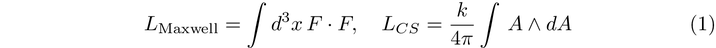
The expression on the left represents the familiar Maxwell term, which lacks dependence on the gauge potential ( A ), indicating its inherent gauge invariance. Conversely, the Chern-Simons term on the right depends explicitly on the gauge potential ( A ), suggesting that it would generally not be gauge invariant. Notably, a coefficient ( k ) accompanies the Chern-Simons term, which we will find must be quantized.

To understand this, we need to analyze a gauge transformation of ( L_{CS} ). Although I won't delve into excessive technical details, we start by considering a gauge transformation resembling winding. This entails a gauge transformation where the time component winds around a circle. Why is periodicity in time achievable? We can perform a Wick rotation and reparameterize time accordingly.

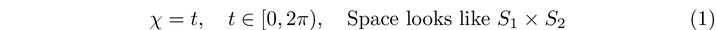
This gauge transformation indicates that the ( A_0 ) component of the gauge potential is also periodic. An explicit calculation of the action under this transformation reveals that it shifts by ( 2pi ) multiplied by an integer quantity—specifically the level itself. In this calculation, one must determine the minimal flux in a small region that results from the Chern-Simons term. This phenomenon is referred to as flux quantization, which can be analyzed by integrating charge around a magnetic monopole. From this small flux, we derive that the Chern-Simons term in this limited region evaluates to the expression below:

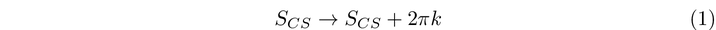
Ultimately, the physical quantity of interest is the partition function, which necessitates that the level of a Chern-Simons term be an integer.

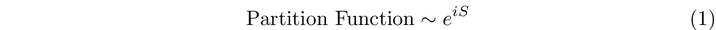
One of the advantages of the Chern-Simons term is that instead of representing it solely as a term in three dimensions, it can also be expressed as a boundary term in four-dimensional space. The left side illustrates the original Chern-Simons term in three-dimensional space.

Chapter 2: Yang-Mills Theory

Yang-Mills theory represents an SU(2) gauge theory. SU(2) is the Lie group composed of special unitary matrices of dimension two. By associating SU(2) with the base space ( mathbb{R}^n ), we create a fiber bundle. Given that ( mathbb{R}^n ) is contractible, it implies the existence of a singular gauge potential—unlike in the case of magnetic monopoles where two gauge potentials exist. SU(2) is generated by three elements, enabling us to express our single gauge potential in the following form:

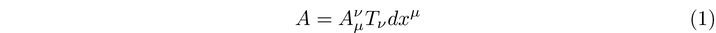
This leads us to define the field strength tensor and the Yang-Mills action.