# Discovering Logarithms Using a Simple String Technique
Written on
Chapter 1: The Catenary and Logarithms
In the realm of mathematics, there's a fascinating method for calculating the logarithm of any number using just a piece of string. This technique is rooted in the concept of the catenary, a term derived from the Latin word for "hanging chain."
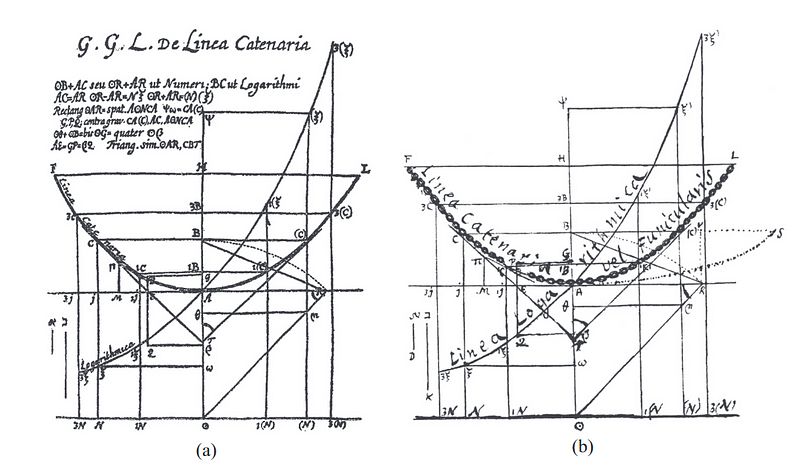
Leibniz's Insights on the Catenary
The renowned German mathematician Gottfried Wilhelm Leibniz once devised an ingenious approach to calculating logarithms that can be performed with nothing more than a length of string. He noted its utility for travelers who might misplace their logarithm tables, suggesting that the catenary could serve as a practical alternative.
> "At that time, Leibniz referred to his discovery as a remarkable and elegant relationship between the curve of a chain and logarithms."
In this section, we will uncover the remarkable technique he proposed for determining the logarithm of any number using the catenary.
The catenary is the shape formed by a freely hanging chain suspended from two points. Interestingly, this curve can be mathematically described within a specific coordinate system.
Chapter 2: Steps to Calculate Logarithms
Step 1: Setting Up the Chain
To begin, suspend a chain from two nails positioned horizontally. Draw a horizontal line through the endpoints of the chain and a vertical line through the lowest point of the chain.
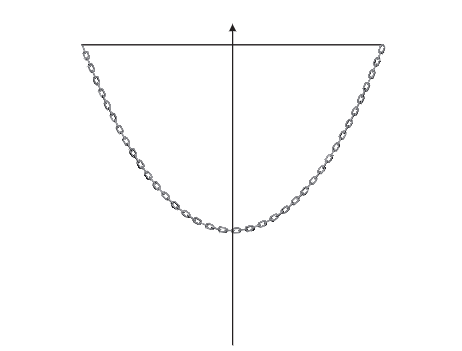
Step 2: Extending the Catenary
Next, place a third nail at the lowest point of the chain and extend one side of the catenary horizontally.
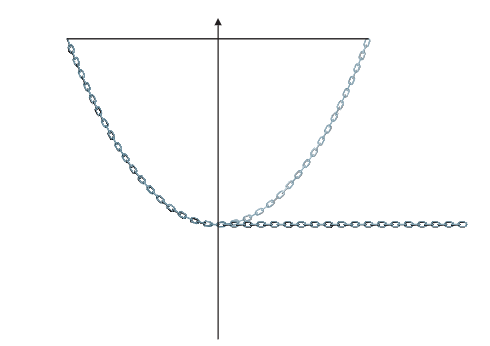
Step 3: Establishing Unit Length
Now, connect the endpoint of the chain to the midpoint of the previously drawn horizontal line. Bisect this segment, and drop a perpendicular line from this point. Draw a horizontal line through the intersection of this perpendicular with the vertical axis. The distance from the origin of this new coordinate system to the lowest point of the catenary will be your unit length, marked in yellow.
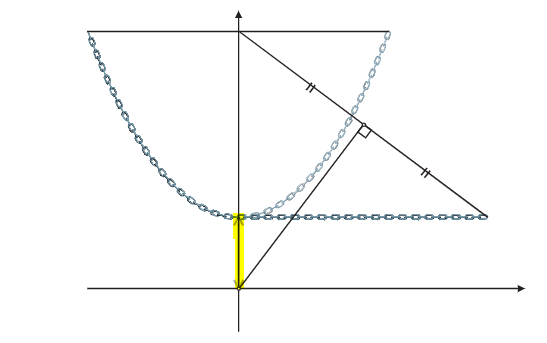
Step 4: Catenary Equation in New Coordinates
Through this process, the catenary can be described mathematically in the new coordinate system.
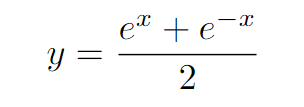
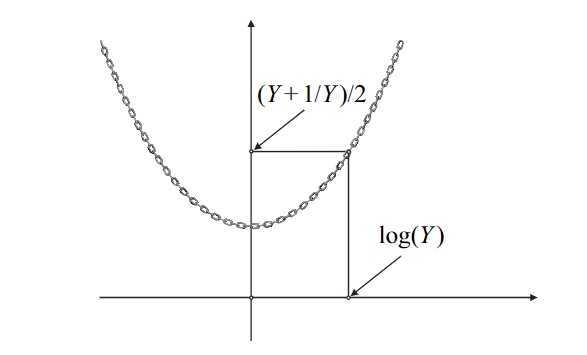
To calculate log(Y), identify (Y + 1/Y)/2 along the y-axis and measure the corresponding x-value, assuming that Y > 1.
Exploring Negative Values
For logarithms of negative numbers, you can apply the same foundational principles.
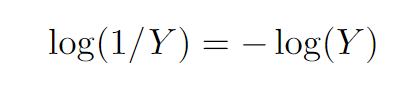
If you're attempting to find the logarithm of a significantly large number, you may discover yourself quite high on the y-axis!
Now, gather a chain and try this method yourself!

Conclusion: Your Experience Matters!
How intriguing is this method? Have you successfully calculated any logarithms? Share your experiences in the comments below; I am eager to hear from you!
To keep up with more captivating math puzzles and narratives, consider subscribing to my email list.
The second video titled "How To Find Log Values | Logarithm of Any Number" provides additional insights into finding logarithmic values effectively.
Thank you for reading! If you found this information valuable, please give a clap to show your appreciation.

Your support means a lot. If you're feeling generous, consider buying me a coffee to help sustain my writing efforts. Happy problem-solving!