Chapter 1: Introduction to the Problem

In this article, we continue our exploration of intriguing questions posed by my students. Today, we will analyze a problem from the 1997 Polish Mathematical Olympiad. We will discuss two distinct methods for tackling this challenge and highlight a valuable general approach applicable to similar problems.

For those interested, you can find all questions from this series, including insights into my inspiration, linked here.

The Olympiad question is stated as follows:

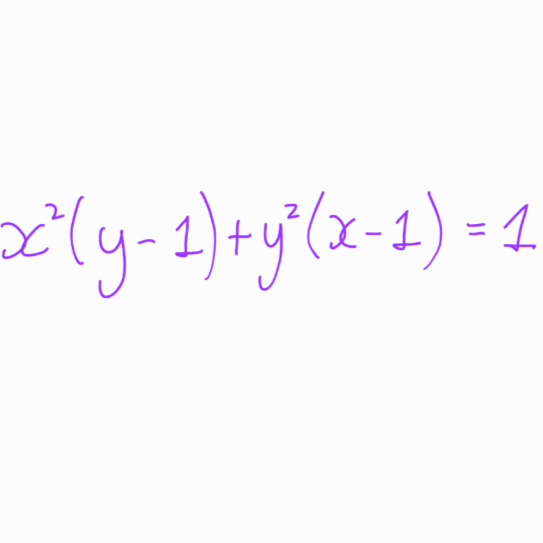
Before proceeding, I encourage you to attempt solving it independently.

Chapter 1.1: Understanding Symmetry in the Equation

One key observation about this equation is its symmetry in the variables x and y. That is, if we interchange x and y, we obtain the same equation because:

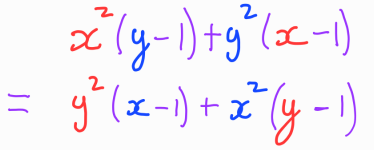
Recognizing that an equation exhibits symmetry can provide crucial insights into potential solving strategies. As mentioned earlier, we will explore two methods to address this problem. The first employs a straightforward technique commonly taught to Math Olympiad participants.

Chapter 1.1.1: Method 1 - A General Approach

When dealing with symmetric equations involving two variables, we can introduce new variables: let ( a = x + y ) and ( b = xy ). The goal is to rewrite the original equation so that it only includes terms of the forms ( x + y ) and ( xy ). Let's proceed with this transformation.

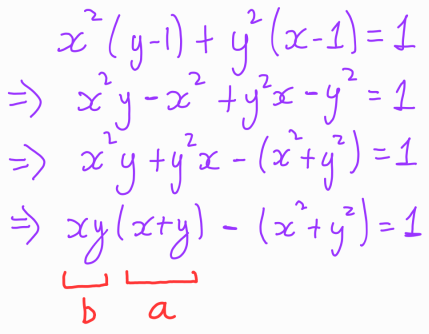
We aim to express ( x^2 + y^2 ) in terms of ( xy ) and ( x + y ). Fortunately, this is manageable since:

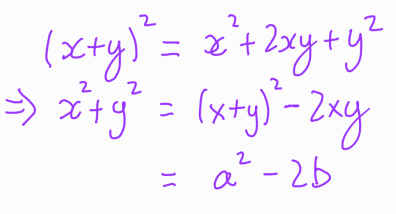
Substituting this back into our original equation yields:

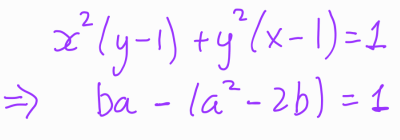
At this point, we can choose to isolate either variable ( a ) or ( b ). For this discussion, we will focus on isolating ( b ). This process isn't overly complex.

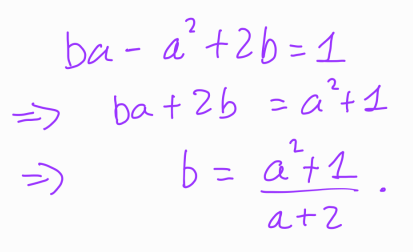
Remember, we are only interested in integer solutions for ( x ) and ( y ), which leads us to concentrate on ( a ) and ( b ). Specifically,

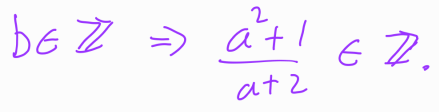
We can tidy up this rational polynomial through either long division or a simple observation that ( a^2 + 1 = a^2 - 4 + 5 ). Both approaches lead us to:

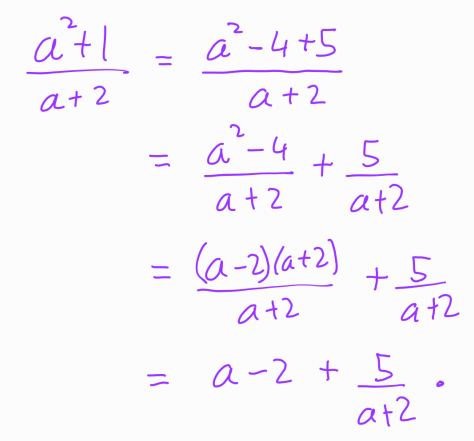
From this, we deduce that:

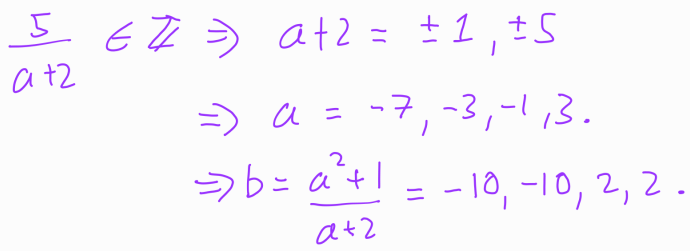
Thus, we arrive at a potential set of solutions expressed in terms of ( a ) and ( b ):

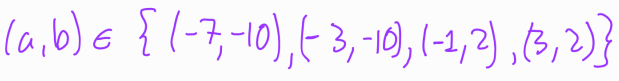
Using the definitions ( a = x + y ) and ( b = xy ), we can now evaluate each solution to determine if they correspond to integer values for ( x ) and ( y ).

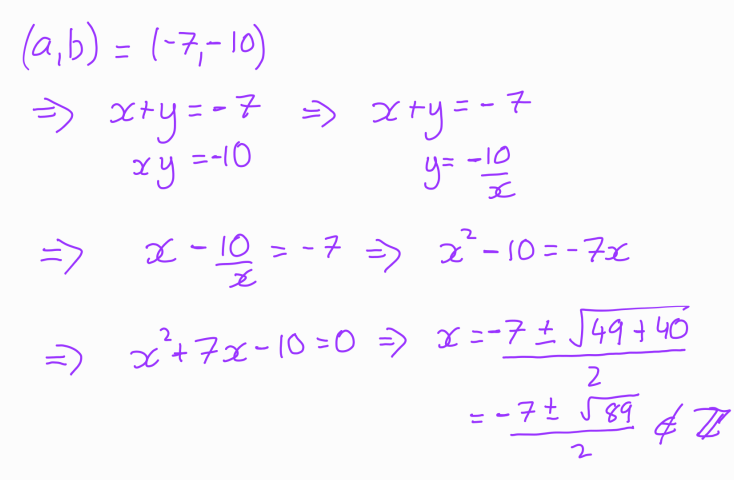
In this case, we find that it does not yield a solution for ( x ) and ( y ). Next, we will explore another potential solution.

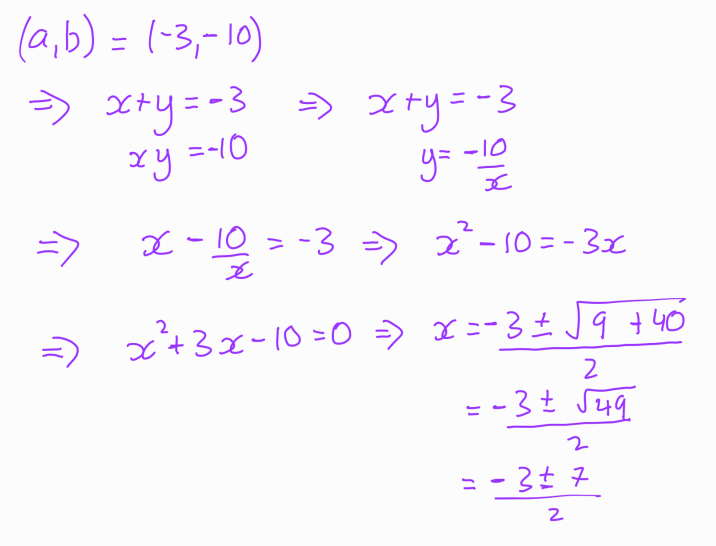
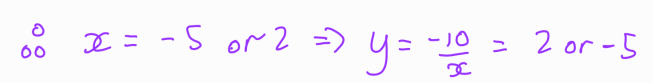
We discover valid solutions here:

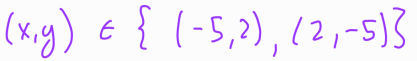
It's noteworthy that these solutions exhibit the expected symmetry, which reinforces their validity. Moving on to the final two potential solutions:

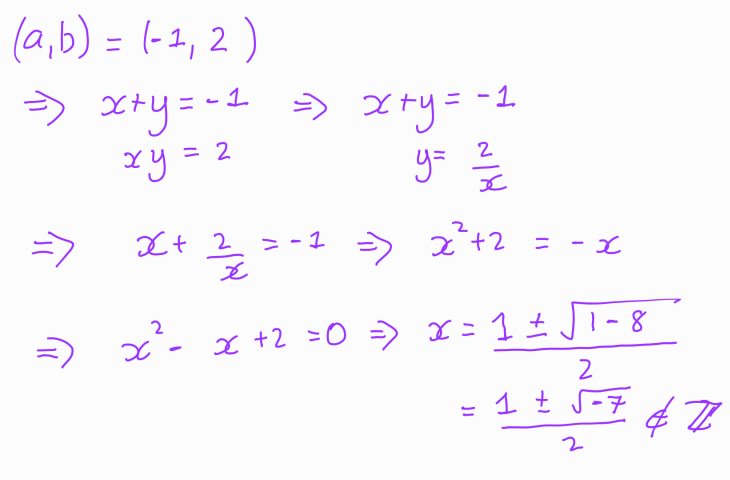
Ultimately, we arrive at:

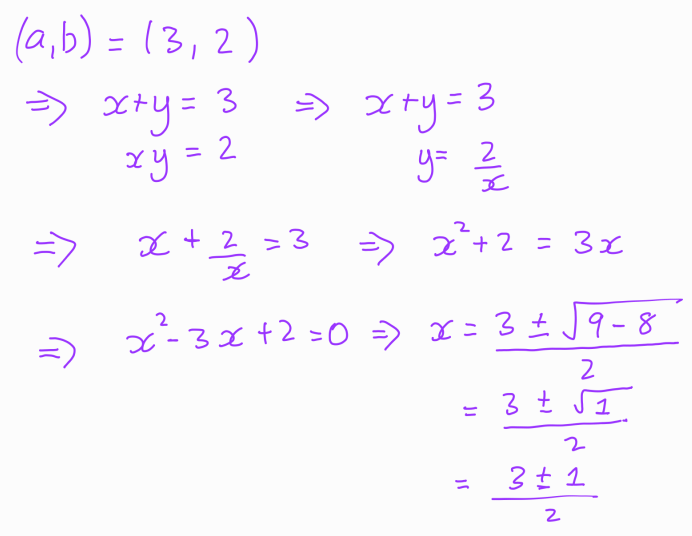
Thus, we conclude with the solution set:

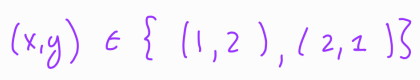
Once again, we observe the symmetry inherent in our solutions. In summary, the only integer solutions to:

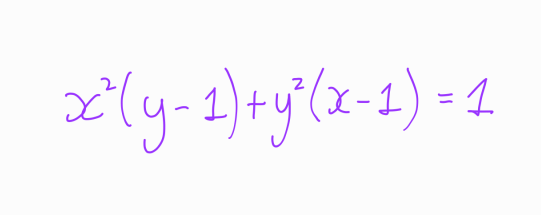
are:

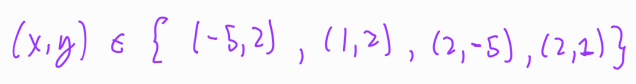
Chapter 2: Method 2 - Alternative Approach

For our second method, we will start by letting ( a = x - 1 ) and ( b = y - 1 ). This leads us to the following expression:

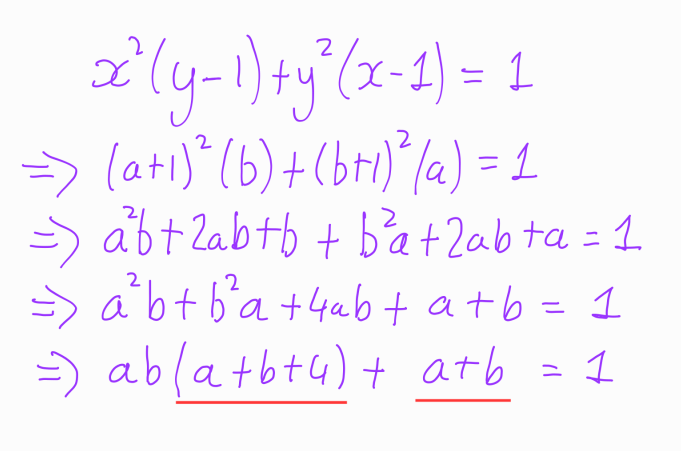
Notice that the two underlined terms are quite similar. If they were identical, we could transform the left-hand side of the equation into a product of two terms. To explore this further, we will add four to both sides:

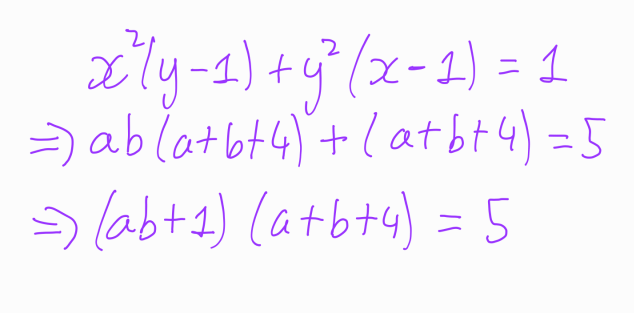
Now, similar to the first method, we recognize that since ( x, y ) are integers, ( a ) and ( b ) must also be integers. Given that 5 is a prime number, we can conclude:

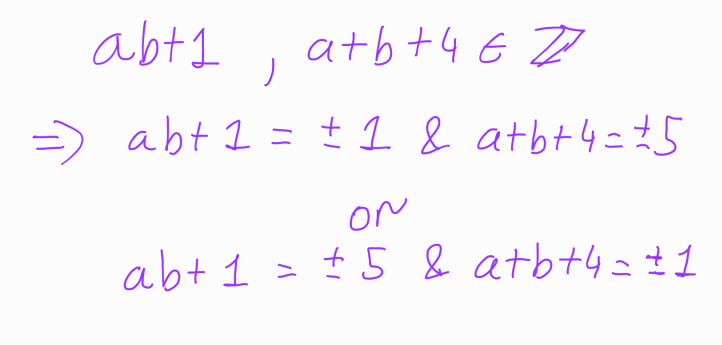
To finalize the second method, we will examine the four possible cases, just as we did in the first method. I encourage readers to verify that this approach yields the same collection of solutions.

Chapter 3: Challenge

Recall that in the first method, we obtained the equation:

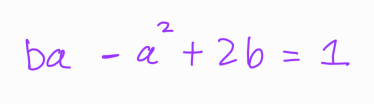
We opted to isolate ( b ) rather than ( a ) simply because it was more straightforward. However, one could choose to isolate ( a ), and upon rewriting the equation as a quadratic in ( a ), one would find:

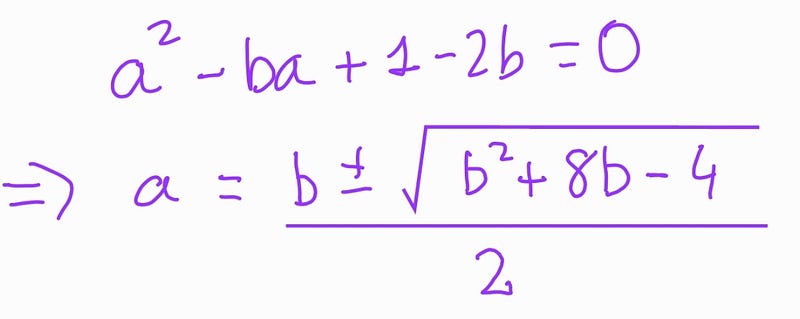
From here, similar to before, we can conclude that:

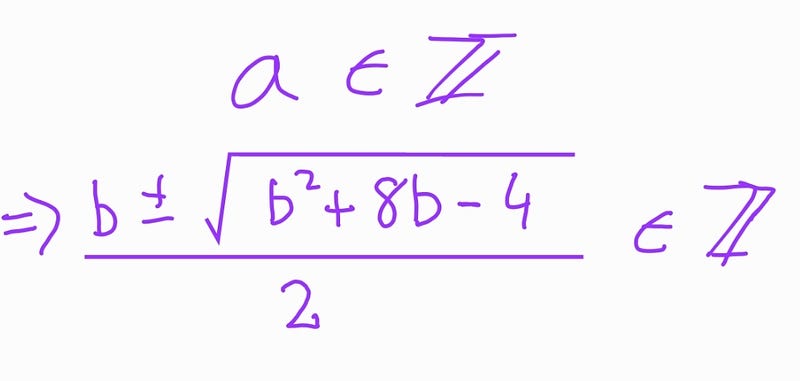
Your challenge is to solve the question from this point onward. Any method I’ve utilized has been, let’s say, less than elegant. I wish you the best of luck!

One remarkable solution has already been provided by Hamid Saadi in the comments section. If you have another approach, please share it as well.

Thank you for reading. I would greatly appreciate your support by following me and my publication Y(Math) to help my articles reach a broader audience. You can join Medium with my referral link to support me and other writers you enjoy.